√Pembahasan Soal Dinamika Partikel ⊗ Full Pembahasanya
Pembahasan soal dinamika partikel
1. Soal UN 2005/2006
Balok A yang massanya 5 kg, diletakkan pada bidang datar yang licin, balok B yang massanya 3 kg digantung dengan tali dan dihubungkan dengan balok A melalui sebuah katrol, jika g = 10 m/s2 tentukan percepatan balok tersebut!
A. 3,50 m/s2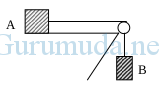
B. 3,75 m/s2
C. 4,00 m/s2
D. 5,00 m/s2
E. 5,25 m/s2
Pembahasan
Diketahui :
Bidang datar licin.
Massa balok A (mA) = 5 kg
Massa balok B (mB) = 3 kg
Percepatan gravitasi (g) = 10 m/s2
Berat balok B (wB) = mB g = (3)(10) = 30 Newton
Ditanya : Percepatan balok (a)
Jawab :
Bidang datar licin sehingga tidak ada gaya gesek yang menghambat gerakan balok A. Gaya yang menggerakan sistem balok adalah gaya berat balok B.
ΣF = m a
wB = (mA + mB) a
30 = (5 + 3) a
30 = 8 a
a = 30 / 8
a = 3,75 m/s2
Jawaban yang benar adalah B.
2. Soal UN 2007/2008 P4 No.7
Berdasar gambar, diketahui :
(1) percepatan benda nol
(2) benda bergerak lurus beraturan
(3) benda dalam keadaan diam
(4) benda akan bergerak jika berat benda lebih kecil dari gaya tariknya
Pernyataan benar adalah….
A. (1) dan (2) saja
B. (1) dan (3) saja
C. (1) dan (4)
D. (1), (2) dan (3) saja
E. (1), (2), (3) dan (4)
Pembahasan
(1) percepatan benda nol
Percepatan benda nol jika resultan gaya sama dengan nol. Resultan gaya :
∑F = m a 
percepatan (a) = 0
∑F = 0
F1 + F2 – F3 = 12 + 24 – 36 = 36 – 36 = 0 N
(2) benda bergerak lurus beraturan
Percepatan benda nol bisa berarti benda diam atau benda bergerak lurus beraturan (benda bergerak dengan kecepatan tetap).
(3) benda dalam keadaan diam
Resultan gaya nol bisa berarti benda sedang diam.
(4) benda akan bergerak jika berat benda lebih kecil dari gaya tariknya
Berat benda bekerja pada arah vertikal, sedangkan gaya tarik bergerak pada arah horisontal. Karena bergerak pada arah horisontal maka hanya gaya-gaya pada arah horisontal yang mempengaruhi benda.
Jawaban yang benar adalah D.
3. Soal UN 2008/2009 P77
Perhatikan gambar di samping!
Jika koefisien gesek kinetik antara balok A dan meja 0,1 dan percepatan gravitasi 10 m s-2 maka gaya yang harus diberikan pada A agar sistem bergerak ke kiri dengan percepata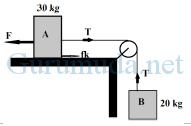
n 2 m s-2 adalah ….
A. 70 N
B. 90 N
C. 150 N
D. 250 N
E. 330 N
Pembahasan
Diketahui :
Massa balok A (mA) = 30 kg
Berat balok A (wA) = (30 kg)(10 m/s2) = 300 kg m/s2 atau 300 Newton
Massa balok B (mB) = 20 kg
Berat balok B (wB) = (20 kg)(10 m/s2) = 200 kg m/s2 atau 200 Newton
Percepatan gravitasi (g) = 10 m/s2
Koefisien gesek kinetis (
) = 0,1
Percepatan sistem (a) = 2 m/s2 (arah percepatan ke kiri)
Gaya gesek kinetis (fk) = N = wA = (0,1)(300) = 30 Newton
Ditanya : Besar gaya F ?
Jawab :
Hukum II Newton :
ΣF = m a
Sistem bergerak ke kiri
F – fk – wB = (mA + mB) a
F – 30 – 200 = (30 + 20)(2)
F – 230 = (50)(2)
F – 230 = 100
F = 230 + 100
F = 330 Newton
Jawaban yang benar adalah E.
4. Soal UN 2008/2009 P45 No.4
Dua benda A dan B masing-masing bermassa 2 kg dan 6 kg diikat dengan tali melalui sebuah katrol yang licin seperti gambar. Mula-mula benda B ditahan kemudian dilepaskan. Jika g = 10 ms-2 maka percepatan benda B adalah…
A. 8,0 ms-2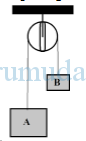
B. 7,5 ms-2
C. 6,0 ms-2
D. 5,0 ms-2
E. 4,0 ms-2
Pembahasan
Diketahui :
mA = 2 kg, mB = 6 kg, g = 10 m/s2
wA = (mA)(g) = (2)(10) = 20 N
wB = (mB)(g) = (6)(10) = 60 N
Ditanya : percepatan benda B atau percepatan sistem ?
Jawab :
wB > wA karenanya benda B bergerak ke bawah, benda A bergerak ke atas (sistem bergerak searah putaran jarum jam).
ΣF = m a
wB – wA = (mA + mB) a
60 – 20 = (2 + 6) a
40 = (8) a
a = 5 m/s2
Jawaban yang benar adalah D.
5. Soal UN 2009/2010 P70 No.11
Benda bermassa dan dihubungkan dengan tali melalui katrol licin seperti gambar. Jika m1 = 1 kg, m2 = 2 kg, dan g = 10 ms-2, maka tegangan T sebesar ….
A. 10,2 N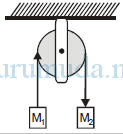 
B. 13,3 N
C. 15,5 N
D. 18,3 N
E. 20,0 N
Pembahasan
Diketahui :
m1 = 1 kg, m2 = 2 kg, g = 10 m/s2
w1 = m1 g = (1 kg)(10 m/s2) = 10 kg m/s2 atau 10 Newton
w2 = m2 g = (2 kg)(10 m/s2) = 20 kg m/s2 atau 20 Newton
Ditanya : gaya tegangan tali (T) ?
Jawab :
w2 > w1 karenanya sistem bergerak searah putaran jarum jam (m2 bergerak ke bawah, m1 bergerak ke atas).
Hukum II Newton :
ΣF = m a
w2 – w1 = (m1 + m2) a
20 – 10 = (1 + 2 ) a
10 = (3) a
a = 3,3 m/s2
Percepatan sistem adalah 3,3 m/s2.
Tegangan tali ?
m2 bergerak ke bawah
w2 – T2 = m2 a
20 – T2 = (2)(3,33)
20 – T2 = 6,66
T2 = 20 – 6,66
T2 = 13,3 Newton
m1 bergerak ke atas
T1 – w1 = m1 a
T1 – 10 = (1)(3,3)
T1 – 10 = 3,33
T1 = 10 + 3,33
T1 = 13,3 Newton
Tegangan tali (T) = 13,3 Newton.
Jawaban yang benar adalah B.
6. Soal UN 2011/2012 A81 No.4
Perhatikan gambar di samping! Massa balok masing-masing m1 = 6 kg dan m2 = 4 kg serta massa katrol diabaikan. Jika permukaan bidang licin dan g = 10 m.s−2, maka percepatan sistem adalah….
A. 0,5 m.s−2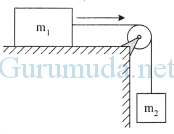
B. 2,0 m.s−2
C. 2,5 m.s−2
D. 4,0 m.s−2
E. 5,0 m.s−2
Pembahasan
Diketahui :
m1 = 6 kg, m2 = 4 kg, g = 10 m/s2
w1 = m1 g = (6 kg)(10 m/s2) = 60 kg m/s2 atau 60 Newton
w2 = m2 g = (4 kg)(10 m/s2) = 40 kg m/s2 atau 40 Newton
Ditanya : percepatan sistem (a) ?
Jawab :
m1 berada di atas permukaan bidang datar licin tanpa gesekan sehingga sistem digerakkan oleh gaya berat balok 2.
Terapkan hukum II Newton :
∑F = m a
w2 = (m1 + m2) a
40 N = (6 kg + 4 kg) a
40 N = (10 kg) a
a = 40 N / 10 kg
a = 4 m/s2
Jawaban yang benar adalah D.
7. Soal UN 2011/2012 C61 No.4
Dua balok yang masing-masing bermassa 2 kg, dihubungkan dengan tali dan katrol seperti pada gambar. Bidang permukaan dan katrol licin. Jika balok B ditarik dengan gaya mendatar 40 N, percepatan balok adalah… (g = 10 m/s2)
A. 5 m/s2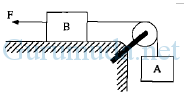
B. 7,5 m/s2
C. 10 m/s2
D. 12,5 m/s2
E. 15 m/s2
Pembahasan :
Diketahui :
mA = mB = 2 kg, g = 10 m/s2, F = 40 N
wA = m g = (2)(10) = 20 N
Ditanya : percepatan balok (a) ?
Jawab :
Permukaan balok licin karenanya gaya yang mempengaruhi gerakan balok hanya gaya F dan gaya berat balok A.
Terapkan hukum II Newton :
∑F = m a
F – wA = (mA + mB) a
40 – 20 = (2 + 2) a
20 = (4) a
a = 20 / 4
a = 5 m/s2
Jawaban yang benar adalah A.
8. Soal UN Fisika SMA 2012/2013 SA 55 No.6
Dari gambar berikut, balok A mempunyai massa 2 kg dan balok B = 1 kg. Balok B mula-mula diam dan kemudian bergerak ke bawah sehingga menyentuh lantai. Bila g = 10 m.s-2, nilai tegangan tali T adalah…
A. 20,0 Newton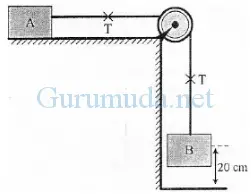
B. 10,0 Newton
C. 6,7 Newton
D. 3,3 Newton
E. 1,7 Newton
Pembahasan
Diketahui :
Massa balok A (mA) = 2 kg
Massa balok B (mB) = 1 kg
Percepatan gravitasi (g) = 10 m/s2
Berat balok B (wB) = mB g = (1)(10) = 10 Newton
Ditanya : Nilai tegangan tali (T)
Jawab :
Pada soal tidak ada keterangan mengenai gesekan karenanya abaikan saja gesekan.
Percepatan sistem (a)
Terlebih dahulu hitung percepatan sistem menggunakan rumus hukum II Newton. Balok B digantung sehingga terdapat gaya berat balok B yang menggerakan balok B ke bawah. Balok B dan balok A dihubungkan dengan tali sehingga balok B menarik balok A hingga keduanya bergerak bersama-sama. Bedanya balok B bergerak ke bawah dan balok A bergerak ke kanan. Hanya ada satu gaya yang sejajar dengan gerakan kedua balok yakni gaya berat balok B (wB). Gaya berat balok A tegak lurus arah gerakan balok A sehingga tidak diperhitungkan dalam menyelesaikan soal. Gaya tegangan tali mempunyai besar sama sepanjang tali dan arahnya berlawanan sehingga saling meniadakan.
∑F = m a
wB = (mA + mB) a
10 = (2 + 1) a
10 = 3 a
a = 10/3
Tegangan tali (T)
Tegangan tali dihitung dengan meninjau masing-masing balok secara terpisah.
Tegangan tali pada balok A
∑F = m a
T = mA a = (2)(10/3) = 20/3 = 6,7 Newton
Tegangan tali pada balok B
∑F = m a
wB – T = mB a
10 – T = (1)(10/3)
10 – T = 3,3
T = 10 – 3,3 = 6,7 Newton
Gaya tegangan tali (T) = 6,7 Newton
Jawaban yang benar adalah C.
9. Soal UN Fisika SMA 2012/2013 SA 60 No.6
Dari gambar berikut, balok A mempunyai massa 2 kg dan balok B = 1 kg. Bila gaya gesekan antara benda A dengan bidang 2,5 Newton, sedangkan gaya gesekan tali dengan katrol diabaikan, maka percepatan kedua benda adalah…
A. 20,0 m.s-2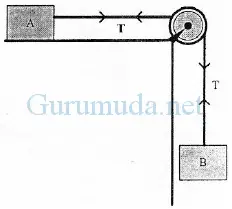
B. 10,0 m.s-2
C. 6,7 m.s-2
D. 3,3 m.s-2
E. 2,5 m.s-2
Pembahasan
Diketahui :
Massa balok A (mA) = 2 kg
Massa balok B (mB) = 1 kg
Gaya gesek antara balok A dan bidang datar (fges A) = 2,5 Newton
Percepatan gravitasi (g) = 10 m/s2
Berat balok B (wB) = mB g = (1)(10) = 10 Newton
Ditanya : Percepatan kedua benda (a)
Jawab :
Percepatan kedua benda dihitung menggunakan rumus hukum II Newton.
∑F = m a
wB – fges = (mA + mB) a
10 – 2,5 = (2 + 1) a
7,5 = 3 a
a = 7,5 / 3 = 2,5 m/s2
Jawaban yang benar adalah E.
10. Soal UN Fisika SMA 2012/2013 SA 65 No.6
Perhatikan gambar! Balok A bermassa 30 kg yang diam di atas lantai licin dihubungkan dengan balok B bermassa 10 kg melalui sebuah katrol. Balok B mula-mula ditahan kemudian dilepaskan sehingga bergerak turun. Percepatan sistem adalah… (g = 10 ms-2)
A. 2,5 ms-2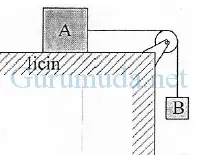
B. 10 ms-2
C. 12 ms-2
D. 15 ms-2
E. 18 ms-2
Pembahasan
Diketahui :
Massa balok A (mA) = 30 kg
Massa balok B (mB) = 10 kg
Percepatan gravitasi (g) = 10 m/s2
Berat balok B (wB) = mB g = (10)(10) = 100 Newton
Ditanya : Percepatan sistem (a)
Jawab :
∑F = m a
wB = (mA + mB) a
100 = (30 + 10) a
100 = 40 a
a = 100 / 40
a = 2,5 m/s2
Jawaban yang benar adalah A.
Hukum Gerak Newton 216.21 KB
Pembahasan soal dinamika rotasi
Momen Gaya
1. Soal UN 2010/2011 P25
Sebuah batang yang sangat ringan, panjangnya 140 cm. Pada batang bekerja tiga gaya masing-masing F1 = 20 N, F2 = 10 N, dan F3 = 40 N dengan arah dan posisi seperti pada gambar. Besar momen gaya yang menyebabkan batang berotasi pada pusat massanya adalah …
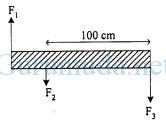
A. 40 N.m
B. 39 N.m
C. 28 N.m
D. 14 N.m
E. 3 N.m
Pembahasan
Diketahui :
Pusat massa batang berada di tengah-tengah batang.
Panjang batang (l) = 140 cm = 1,4 meter
Gaya 1 (F1) = 20 N, lengan gaya 1 (l1) = 70 cm = 0,7 meter
Gaya 2 (F2) = 10 N, lengan gaya 2 (l2) = 100 cm – 70 cm = 30 cm = 0,3 meter
Gaya 3 (F3) = 40 N, lengan gaya 3 (l3) = 70 cm = 0,7 meter
Ditanya : Besar momen gaya yang menyebabkan batang berotasi pada pusat massanya
Jawab :
Momen gaya 1 menyebabkan batang berotasi searah putaran jarum jam. Karenanya momen gaya 1 bertanda negatif.
τ1 = F1 l1 = (20 N)(0,7 m) = -14 N m
Momen gaya 2 menyebabkan batang berotasi berlawanan arah putaran jarum jam. Karenanya momen gaya 2 bertanda positif.
τ2 = F2 l2 = (10 N)(0,3 m) = 3 N m
Momen gaya 3 menyebabkan batang berotasi searah putaran jarum jam. Karenanya momen gaya 3 bertanda negatif.
τ3 = F3 l3 = (40 N)(0,7 m) = -28 N m
Resultan momen gaya :
Στ = -14 Nm + 3 Nm – 28 Nm = – 42 Nm + 3 Nm = -39 Nm
Besar momen gaya adalah 39 Newton meter. Bertanda negatif artinya arah rotasi batang searah dengan putaran jarum jam.
Jawaban yang benar adalah B.
2. Soal UN 2011/2012 B74 No.7
Batang AB yang massanya diabaikan diletakkan mendatar dan dikerjakan tiga buah gaya seperti gambar. Resultan momen gaya yang bekerja pada batang jika diputar pada poros di D adalah… (sin 53o = 0,8)
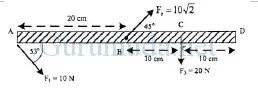
A. 2,4 N m
B. 2,6 N m
C. 3,0 N m
D. 3,2 N m
E. 3,4 N m
Pembahasan
Diketahui :
Sumbu rotasi atau poros terletak di titik D.
F1 = 10 N dan l1 = r1 sin θ = (40 cm)(sin 53o) = (0,4 m)(0,8) = 0,32 meter
F2 = 10√2 N dan l2 = r2 sin θ = (20 cm)(sin 45o) = (0,2 m)(0,5√2) = 0,1√2 meter
F3 = 20 N dan l3 = r1 sin θ = (10 cm)(sin 90o) = (0,1 m)(1) = 0,1 meter
Ditanya : Resultan momen gaya
Jawab :
τ1 = F1 l1 = (10 N)(0,32 m) = 3,2 Nm
(positif karena momen gaya ini menyebabkan balok berotasi berlawanan dengan arah putaran jarum jam)
τ1 = F2 l2 = (10√2 N)( 0,1√2 m) = -2 Nm
(negatif karena momen gaya ini menyebabkan balook berotasi searah putaran jarum jam)
τ1 = F2 l2 = (20 N)(0,1 m) = 2 Nm
(positif karena momen gaya ini menyebabkan balok berotasi berlawanan dengan arah putaran jarum jam)
Resultan momen gaya :
Στ = τ1 – τ1 + τ3
Στ = 3,2 Nm – 2 Nm + 2 Nm
Στ = 3,2 Nm
Jawaban yang benar adalah D.
3. Soal UN Fisika SMA 2012/2013 SA 55 No.8
Batang AB yang massanya diabaikan diletakkan mendatar dan dikerjakan tiga buah gaya seperti gambar. Resultan momen gaya yang bekerja pada batang jika diputar pada poros di D adalah… (sin 53o = 0,8)
A. 2,4 N.m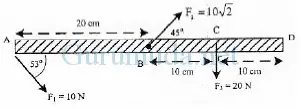
B. 2,6 N.m
C. 3,0 N.m
D. 3,2 N.m
E. 3,4 N.m
Pembahasan
Diketahui :
Sumbu rotasi terletak di D.
Jarak antara F1 dan sumbu rotasi (rAD) = 40 cm = 0,4 m
Jarak antara F2 dan sumbu rotasi (rBD) = 20 cm = 0,2 m
Jarak antara F3 dan sumbu rotasi (rCD) = 10 cm = 0,1 m
F1 = 10 Newton
F2 = 10√2 Newton
F3 = 20 Newton
Sin 53o = 0,8
Ditanya : Resultan momen gaya jika batang diputar pada poros di D
Jawab :
Hitung momen gaya yang ditimbulkan oleh masing-masing gaya.
Momen gaya 1
Στ1 = (F1)(rAD sin 53o) = (10 N)(0,4 m)(0,8) = 3,2 N.m
Momen gaya 1 bertanda positif karena arah rotasi batang yang ditimbulkan oleh momen gaya 1 berlawanan arah dengan putaran jarum jam.
Momen gaya 2
Στ2 = (F2)(rBD sin 45o) = (10√2 N)(0,2 m)(0,5√2) = -2 N.m
Momen gaya 2 bertanda negatif karena arah rotasi batang yang ditimbulkan oleh momen gaya 2 searah dengan putaran jarum jam.
Momen gaya 3
Στ3 = (F3)(rCD sin 90o) = (20 N)(0,1 m)(1) = 2 N.m
Momen gaya 3 bertanda positif karena arah rotasi batang yang ditimbulkan oleh momen gaya 3 berlawanan arah dengan putaran jarum jam.
Resultan momen gaya
Στ = Στ1 + Στ2 + Στ3
Στ = 3,2 – 2 + 2
Στ = 3,2 Newton meter
Jawaban yang benar adalah D.
Momen Inersia
4. Soal UN Fisika SMA 2012/2013 SA 65 No.7
Perhatikan gambar dua bola yang dihubungkan dengan seutas kawat. Panjang kawat = 12 m, l1 = 4 m dan massa kawat diabaikan, maka besarnya momen inersia sistem adalah…
A. 52,6 kg m2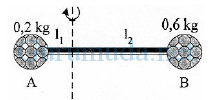
B. 41,6 kg m2
C. 34,6 kg m2
D. 22,4 kg m2
E. 20,4 kg m2
Pembahasan
Diketahui :
Massa bola A (mA) = 0,2 kg
Massa bola B (mB) = 0,6 kg
Jarak antara bola A dan sumbu rotasi (rA) = 4 meter
Jarak antara bola B dan sumbu rotasi (rB) = 12 – 4 = 8 meter
Ditanya : Momen inersia (I) sistem
Jawab :
Momen inersia bola A
IA = (mA)(rA2) = (0,2)(4)2 = (0,2)(16) = 3,2 kg m2
Momen inersia bola B
IB = (mB)(rB2) = (0,6)(8)2 = (0,6)(64) = 38,4 kg m2
Momen inersia sistem partikel :
I = IA + IB = 3,2 + 38,4 = 41,6 kg m2
Jawaban yang benar adalah B.
Hukum II Newton Gerak Rotasi
5. Soal EBTANAS Fisika SMA Tahun 2000 No. 27
Perhatikan gambar sebuah roda pejal homogen di samping ini. Pada tepi roda dililitkan sebuah tali dan kemudian ujung tali ditarik dengan gaya F sebesar 6 N. Jika massa roda 5 kg dan jari-jarinya 20 cm, percepatan sudut roda tersebut adalah…
A. 0,12 rad s–2
B. 1,2 rad s–2
C. 3,0 rad s–2
D. 6,0 rad s–2
E. 12,0 rad s–2
Pembahasan
Diketahui :
Gaya tarik (F) = 6 Newton
Massa roda (M) = 5 kg
Jari-jari roda (R) = 20 cm = 20/100 m = 0,2 m
Ditanya : Percepatan sudut roda (α)
Jawab :
Hitung momen gaya :
τ = F R = (6 Newton)(0,2 meter) = 1,2 Newton meter
Hitung momen inersia :
Rumus momen inersia roda pejal berbentuk cakram atau piringan adalah 1/2 M R2 = 1/2 (5 kg)(0,2 m)2 = 1/2 (5 kg)(0,04 m2) = 1/2 (0,2) = 0,1 kg m2.
Hitung percepatan sudut menggunakan rumus dinamika rotasi :
τ = I α
α = τ / I = 1,2 / 0,1 = 12 rad s-2
Jawaban yang benar adalah E.
6. Soal UN 2000/2001
Sebuah katrol cakram pejal massanya 8 kg dan berjari-jari 10 cm pada tepinya dililitkan seutas tali yang ujungnya diikatkan beban 4 kg (g = 10 ms-2 ). Percepatan gerak turunnya beban adalah …
A. 2,5 ms–2
B. 5,0 ms–2
C. 10,0 ms–2
D. 20,0 ms–2
E. 33,3 ms–2
Pembahasan
Diketahui :
Massa katrol cakram pejal (m) = 8 kg
Jari-jari katrol cakram pejal (r) = 10 cm = 0,1 meter
Massa beban (m) = 4 kg
Percepatan gravitasi (g) = 10 m/s2
Berat beban (w) = m g = (4 kg)(10 m/s2) = 40 kg m/s2 = 40 Newton
Ditanya : Percepatan gerak turunnya beban
Jawab :
Hitung momen inersia cakram pejal :
I = 1/2 M R2 = 1/2 (8 kg)(0,1 m)2 = (4 kg)(0,01 m2) = 0,04 kg m2
Hitung momen gaya :
τ = F r = (40 N)(0,1 m) = 4 Nm
Hitung percepatan sudut menggunakan rumus hukum II Newton untuk gerak rotasi :
Στ = I α
4 = 0,04 α
α = 4 / 0,04 = 100
Hitung percepatan gerak turunnya beban :
a = r α = (0,1)(100) = 10 m/s2
Jawaban yang benar adalah C.
7. Soal UN 2008/2009 P04 No. 8
Sebuah katrol pejal bermassa (M) dan jari-jarinya (R) seperti pada gambar! Salah satu ujung tali tak bermassa dililitkan pada katrol, ujung tali yang lain digantungi beban m kg percepatan sudut katrol (α) jika beban dilepas. Jika pada katrol ditempelkan plastisin A yang bermassa 1⁄2 M, untuk menghasilkan percepatan sudut yang sama beban harus dijadikan…. (I katrol = 1/2 MR2)
A. 3/4 m kg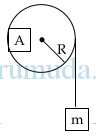
B. 3/2 m kg
C. 2 m kg
D. 3 m kg
E. 4 m kg
Pembahasan
Diketahui :
massa beban = m
Berat beban = w = m g
Massa katrol pejal = M
Jari-jari katrol pejal = R
Percepatan sudut katrol = α
Ditanya :
Jika massa katrol bertambah menjadi M + M/2 = 3M/2 dan percepatan sudut katrol = α, berapa massa beban ?
Jawab :
Momen inersia katrol tanpa plastisin :
I = 1/2 M R2 = 0,5 M R2
Momen inersia katrol + plastisin :
I = 1/2 (3M/2) R2 = (3M/4) R2 = 0,75M R2
Momen gaya :
τ = F R
Rumus hukum II Newton gerak rotasi :
Στ = I α
w R = I α
m g R = I α
α = m g R / I
Untuk menghasilkan percepatan sudut yang sama, massa beban harus dijadikan….. Subtitusikan α pada persamaan 2 dengan α pada persamaan 1 :
Jawaban yang benar adalah B.
8. Soal UN 2009/2010 P12 No.7
Sebuah katrol dari benda pejal dengan tali yang dililitkan pada sisi luarnya ditampilkan seperti gambar. Gesekan katrol dengan tali dan gesekan di sumbu putarnya diabaikan. Jika beban bergerak turun dengan percepatan tetap a ms-2, maka nilai momen inersia katrol setara dengan….
A. I = τ α R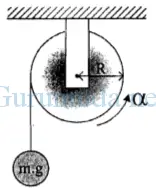
B. I = τ α-1 R
C. I = τ a R
D. I = τ a-1 R-1
E. I = τ a R-1
Pembahasan
Diketahui :
Gaya = w = m g
Lengan gaya = R
Percepatan sudut = α
Percepatan beban = a ms-2
Ditanya : Momen inersia katrol (I)
Jawab :
Hubungan antara percepatan linear dan percepatan sudut :
a = R α
α = a / R
Momen inersia dihitung menggunakan rumus :
τ = I α
I = τ : α = τ : a / R = τ (R / a) = τ R a-1
Tidak ada jawaban yang benar.
9. Soal UN Fisika SMA/MA U-ZC-2013/2014 No.6
Sebuah katrol dari benda pejal dengan tali yang dililitkan pada sisi luarnya ditampilkan seperti gambar. Gesekan katrol diabaikan. Jika momen inersia katrol I = β dan tali ditarik dengan gaya tetap F, maka nilai F setara dengan….
A. F = α . β . R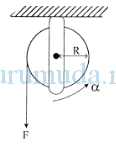 
B. F = α . β 2 . R
C. F = α . (β . R)-1
D. F = α . β . (R)-1
E. F = R . (α . β)-1
Pembahasan
Diketahui :
Gaya tarik = F
Momen inersia katrol = β
Percepatan sudut katrol = α
Jari-jari katrol = R
Ditanya : Nilai F setara dengan….
Jawab :
Rumus hukum II Newton pada gerak rotasi :
Στ = β α ———- Persamaan 1
Keterangan rumus :
Στ = Resultan momen gaya (torsi)
β = Momen inersia
α = Percepatan sudut
Resultan momen gaya yang bekerja pada katrol :
Στ = F R ———-> Persamaan 2
Keterangan rumus :
F = gaya tarik
R = Jarak titik kerja gaya F ke sumbu rotasi = jari-jari katrol
Gantikan Στ pada persamaan 1 dengan Στ pada persamaan 2 :
Στ = β . α
F . R = β . α
F = (β . α) / R
F = β . α . (R-1)
Jawaban yang benar adalah D.
Momentum Sudut
10. Soal UN 1999/2000 No. 28
Sebuah partikel bermassa 0,2 gram bergerak melingkar dengan kecepatan sudut tetap 10 rad s-1. Jika jari-jari lintasan partikel 3 cm, maka momentum sudut partikel itu adalah …
A. 3 × 10–7 kg m2 s-1
B. 9 × 10–7 kg m2 s-1
C. 1,6 × 10–6 kg m2 s-1
D. 1,8 × 10–4 kg m2 s-1
E. 4,5 × 10–3 kg m2 s-1
Pembahasan
Diketahui :
Massa partikel (m) = 0,2 gram = 2 x 10-4 kg
Kecepatan sudut (ω) = 10 rad s-1
Jari-jari lintasan partikel (r) = 3 cm = 3 x 10-2 meter
Ditanya : Momentum sudut partikel
Jawab :
Rumus momentum sudut :
L = I ω
Keterangan : I momentum sudut, I = momen inersia, ω = kecepatan sudut
Momen inersia partikel :
I = m r2 = (2 x 10-4 )(3 x 10-2)2 = (2 x 10-4 )(9 x 10-4) = 18 x 10-8
Momentum sudut adalah :
L = I ω = (18 x 10-8)(10 rad s-1) = 18 x 10-7 kg m2 s-1
Tidak ada jawaban yang benar.
11. Soal UN 2005/2006
Seorang penari berputar, tangan terentang sepanjang 160 cm. Kemudian tangan dilipat menjadi 80 cm sepanjang siku. Jika kecepatan sudut putar dari penari itu tetap maka momentum liniernya …
A. tetap
B. menjadi 1/2 kali semula
C. menjadi 3/4 kali semula
D. menjadi 2 kali semula
E. menjadi 4 kali semula
Pembahasan
Diketahui :
Jari-jari 1 (r1) = 160 cm
Jari-jari 2 (r2) = 80 cm
Kecepatan sudut 1 (ω1) = ω
Kecepatan sudut 1 (ω2) = ω
Ditanya : Momentum linear
Jawab :
Kecepatan linear 1 :
v1 = r1 ω1 = (160 cm) ω
Kecepatan linear 2 :
v2 = r2 ω2 = (80 cm) ω
Momentum linear 1 :
p = m v1 = m (160 cm) ω
Momentum linear 2 :
p = m v2 = m (80 cm) ω
Jadi momentum linearnya menjadi 1/2 kali semula.
Jawaban yang benar adalah B.
Dinamika rotasi 222.50 KBPembahasan soal dinamika rotasi
Momen Gaya
1. Soal UN 2010/2011 P25
Sebuah batang yang sangat ringan, panjangnya 140 cm. Pada batang bekerja tiga gaya masing-masing F1 = 20 N, F2 = 10 N, dan F3 = 40 N dengan arah dan posisi seperti pada gambar. Besar momen gaya yang menyebabkan batang berotasi pada pusat massanya adalah …
A. 40 N.m
B. 39 N.m
C. 28 N.m
D. 14 N.m
E. 3 N.m
Pembahasan
Diketahui :
Pusat massa batang berada di tengah-tengah batang.
Panjang batang (l) = 140 cm = 1,4 meter
Gaya 1 (F1) = 20 N, lengan gaya 1 (l1) = 70 cm = 0,7 meter
Gaya 2 (F2) = 10 N, lengan gaya 2 (l2) = 100 cm – 70 cm = 30 cm = 0,3 meter
Gaya 3 (F3) = 40 N, lengan gaya 3 (l3) = 70 cm = 0,7 meter
Ditanya : Besar momen gaya yang menyebabkan batang berotasi pada pusat massanya
Jawab :
Momen gaya 1 menyebabkan batang berotasi searah putaran jarum jam. Karenanya momen gaya 1 bertanda negatif.
τ1 = F1 l1 = (20 N)(0,7 m) = -14 N m
Momen gaya 2 menyebabkan batang berotasi berlawanan arah putaran jarum jam. Karenanya momen gaya 2 bertanda positif.
τ2 = F2 l2 = (10 N)(0,3 m) = 3 N m
Momen gaya 3 menyebabkan batang berotasi searah putaran jarum jam. Karenanya momen gaya 3 bertanda negatif.
τ3 = F3 l3 = (40 N)(0,7 m) = -28 N m
Resultan momen gaya :
Στ = -14 Nm + 3 Nm – 28 Nm = – 42 Nm + 3 Nm = -39 Nm
Besar momen gaya adalah 39 Newton meter. Bertanda negatif artinya arah rotasi batang searah dengan putaran jarum jam.
Jawaban yang benar adalah B.
2. Soal UN 2011/2012 B74 No.7
Batang AB yang massanya diabaikan diletakkan mendatar dan dikerjakan tiga buah gaya seperti gambar. Resultan momen gaya yang bekerja pada batang jika diputar pada poros di D adalah… (sin 53o = 0,8)
A. 2,4 N m
B. 2,6 N m
C. 3,0 N m
D. 3,2 N m
E. 3,4 N m
Pembahasan
Diketahui :
Sumbu rotasi atau poros terletak di titik D.
F1 = 10 N dan l1 = r1 sin θ = (40 cm)(sin 53o) = (0,4 m)(0,8) = 0,32 meter
F2 = 10√2 N dan l2 = r2 sin θ = (20 cm)(sin 45o) = (0,2 m)(0,5√2) = 0,1√2 meter
F3 = 20 N dan l3 = r1 sin θ = (10 cm)(sin 90o) = (0,1 m)(1) = 0,1 meter
Ditanya : Resultan momen gaya
Jawab :
τ1 = F1 l1 = (10 N)(0,32 m) = 3,2 Nm
(positif karena momen gaya ini menyebabkan balok berotasi berlawanan dengan arah putaran jarum jam)
τ1 = F2 l2 = (10√2 N)( 0,1√2 m) = -2 Nm
(negatif karena momen gaya ini menyebabkan balook berotasi searah putaran jarum jam)
τ1 = F2 l2 = (20 N)(0,1 m) = 2 Nm
(positif karena momen gaya ini menyebabkan balok berotasi berlawanan dengan arah putaran jarum jam)
Resultan momen gaya :
Στ = τ1 – τ1 + τ3
Στ = 3,2 Nm – 2 Nm + 2 Nm
Στ = 3,2 Nm
Jawaban yang benar adalah D.
3. Soal UN Fisika SMA 2012/2013 SA 55 No.8
Batang AB yang massanya diabaikan diletakkan mendatar dan dikerjakan tiga buah gaya seperti gambar. Resultan momen gaya yang bekerja pada batang jika diputar pada poros di D adalah… (sin 53o = 0,8)
A. 2,4 N.m
B. 2,6 N.m
C. 3,0 N.m
D. 3,2 N.m
E. 3,4 N.m
Pembahasan
Diketahui :
Sumbu rotasi terletak di D.
Jarak antara F1 dan sumbu rotasi (rAD) = 40 cm = 0,4 m
Jarak antara F2 dan sumbu rotasi (rBD) = 20 cm = 0,2 m
Jarak antara F3 dan sumbu rotasi (rCD) = 10 cm = 0,1 m
F1 = 10 Newton
F2 = 10√2 Newton
F3 = 20 Newton
Sin 53o = 0,8
Ditanya : Resultan momen gaya jika batang diputar pada poros di D
Jawab :
Hitung momen gaya yang ditimbulkan oleh masing-masing gaya.
Momen gaya 1
Στ1 = (F1)(rAD sin 53o) = (10 N)(0,4 m)(0,8) = 3,2 N.m
Momen gaya 1 bertanda positif karena arah rotasi batang yang ditimbulkan oleh momen gaya 1 berlawanan arah dengan putaran jarum jam.
Momen gaya 2
Στ2 = (F2)(rBD sin 45o) = (10√2 N)(0,2 m)(0,5√2) = -2 N.m
Momen gaya 2 bertanda negatif karena arah rotasi batang yang ditimbulkan oleh momen gaya 2 searah dengan putaran jarum jam.
Momen gaya 3
Στ3 = (F3)(rCD sin 90o) = (20 N)(0,1 m)(1) = 2 N.m
Momen gaya 3 bertanda positif karena arah rotasi batang yang ditimbulkan oleh momen gaya 3 berlawanan arah dengan putaran jarum jam.
Resultan momen gaya
Στ = Στ1 + Στ2 + Στ3
Στ = 3,2 – 2 + 2
Στ = 3,2 Newton meter
Jawaban yang benar adalah D.
Momen Inersia
4. Soal UN Fisika SMA 2012/2013 SA 65 No.7
Perhatikan gambar dua bola yang dihubungkan dengan seutas kawat. Panjang kawat = 12 m, l1 = 4 m dan massa kawat diabaikan, maka besarnya momen inersia sistem adalah…
A. 52,6 kg m2
B. 41,6 kg m2
C. 34,6 kg m2
D. 22,4 kg m2
E. 20,4 kg m2
Pembahasan
Diketahui :
Massa bola A (mA) = 0,2 kg
Massa bola B (mB) = 0,6 kg
Jarak antara bola A dan sumbu rotasi (rA) = 4 meter
Jarak antara bola B dan sumbu rotasi (rB) = 12 – 4 = 8 meter
Ditanya : Momen inersia (I) sistem
Jawab :
Momen inersia bola A
IA = (mA)(rA2) = (0,2)(4)2 = (0,2)(16) = 3,2 kg m2
Momen inersia bola B
IB = (mB)(rB2) = (0,6)(8)2 = (0,6)(64) = 38,4 kg m2
Momen inersia sistem partikel :
I = IA + IB = 3,2 + 38,4 = 41,6 kg m2
Jawaban yang benar adalah B.
Hukum II Newton Gerak Rotasi
5. Soal EBTANAS Fisika SMA Tahun 2000 No. 27
Perhatikan gambar sebuah roda pejal homogen di samping ini. Pada tepi roda dililitkan sebuah tali dan kemudian ujung tali ditarik dengan gaya F sebesar 6 N. Jika massa roda 5 kg dan jari-jarinya 20 cm, percepatan sudut roda tersebut adalah…
A. 0,12 rad s–2
B. 1,2 rad s–2
C. 3,0 rad s–2
D. 6,0 rad s–2
E. 12,0 rad s–2
Pembahasan
Diketahui :
Gaya tarik (F) = 6 Newton
Massa roda (M) = 5 kg
Jari-jari roda (R) = 20 cm = 20/100 m = 0,2 m
Ditanya : Percepatan sudut roda (α)
Jawab :
Hitung momen gaya :
τ = F R = (6 Newton)(0,2 meter) = 1,2 Newton meter
Hitung momen inersia :
Rumus momen inersia roda pejal berbentuk cakram atau piringan adalah 1/2 M R2 = 1/2 (5 kg)(0,2 m)2 = 1/2 (5 kg)(0,04 m2) = 1/2 (0,2) = 0,1 kg m2.
Hitung percepatan sudut menggunakan rumus dinamika rotasi :
τ = I α
α = τ / I = 1,2 / 0,1 = 12 rad s-2
Jawaban yang benar adalah E.
6. Soal UN 2000/2001
Sebuah katrol cakram pejal massanya 8 kg dan berjari-jari 10 cm pada tepinya dililitkan seutas tali yang ujungnya diikatkan beban 4 kg (g = 10 ms-2 ). Percepatan gerak turunnya beban adalah …
A. 2,5 ms–2
B. 5,0 ms–2
C. 10,0 ms–2
D. 20,0 ms–2
E. 33,3 ms–2
Pembahasan
Diketahui :
Massa katrol cakram pejal (m) = 8 kg
Jari-jari katrol cakram pejal (r) = 10 cm = 0,1 meter
Massa beban (m) = 4 kg
Percepatan gravitasi (g) = 10 m/s2
Berat beban (w) = m g = (4 kg)(10 m/s2) = 40 kg m/s2 = 40 Newton
Ditanya : Percepatan gerak turunnya beban
Jawab :
Hitung momen inersia cakram pejal :
I = 1/2 M R2 = 1/2 (8 kg)(0,1 m)2 = (4 kg)(0,01 m2) = 0,04 kg m2
Hitung momen gaya :
τ = F r = (40 N)(0,1 m) = 4 Nm
Hitung percepatan sudut menggunakan rumus hukum II Newton untuk gerak rotasi :
Στ = I α
4 = 0,04 α
α = 4 / 0,04 = 100
Hitung percepatan gerak turunnya beban :
a = r α = (0,1)(100) = 10 m/s2
Jawaban yang benar adalah C.
7. Soal UN 2008/2009 P04 No. 8
Sebuah katrol pejal bermassa (M) dan jari-jarinya (R) seperti pada gambar! Salah satu ujung tali tak bermassa dililitkan pada katrol, ujung tali yang lain digantungi beban m kg percepatan sudut katrol (α) jika beban dilepas. Jika pada katrol ditempelkan plastisin A yang bermassa 1⁄2 M, untuk menghasilkan percepatan sudut yang sama beban harus dijadikan…. (I katrol = 1/2 MR2)
A. 3/4 m kg
B. 3/2 m kg
C. 2 m kg
D. 3 m kg
E. 4 m kg
Pembahasan
Diketahui :
massa beban = m
Berat beban = w = m g
Massa katrol pejal = M
Jari-jari katrol pejal = R
Percepatan sudut katrol = α
Ditanya :
Jika massa katrol bertambah menjadi M + M/2 = 3M/2 dan percepatan sudut katrol = α, berapa massa beban ?
Jawab :
Momen inersia katrol tanpa plastisin :
I = 1/2 M R2 = 0,5 M R2
Momen inersia katrol + plastisin :
I = 1/2 (3M/2) R2 = (3M/4) R2 = 0,75M R2
Momen gaya :
τ = F R
Rumus hukum II Newton gerak rotasi :
Στ = I α
w R = I α
m g R = I α
α = m g R / I
Untuk menghasilkan percepatan sudut yang sama, massa beban harus dijadikan….. Subtitusikan α pada persamaan 2 dengan α pada persamaan 1 :
Jawaban yang benar adalah B.
8. Soal UN 2009/2010 P12 No.7
Sebuah katrol dari benda pejal dengan tali yang dililitkan pada sisi luarnya ditampilkan seperti gambar. Gesekan katrol dengan tali dan gesekan di sumbu putarnya diabaikan. Jika beban bergerak turun dengan percepatan tetap a ms-2, maka nilai momen inersia katrol setara dengan….
A. I = τ α R
B. I = τ α-1 R
C. I = τ a R
D. I = τ a-1 R-1
E. I = τ a R-1
Pembahasan
Diketahui :
Gaya = w = m g
Lengan gaya = R
Percepatan sudut = α
Percepatan beban = a ms-2
Ditanya : Momen inersia katrol (I)
Jawab :
Hubungan antara percepatan linear dan percepatan sudut :
a = R α
α = a / R
Momen inersia dihitung menggunakan rumus :
τ = I α
I = τ : α = τ : a / R = τ (R / a) = τ R a-1
Tidak ada jawaban yang benar.
9. Soal UN Fisika SMA/MA U-ZC-2013/2014 No.6
Sebuah katrol dari benda pejal dengan tali yang dililitkan pada sisi luarnya ditampilkan seperti gambar. Gesekan katrol diabaikan. Jika momen inersia katrol I = β dan tali ditarik dengan gaya tetap F, maka nilai F setara dengan….
A. F = α . β . R
B. F = α . β 2 . R
C. F = α . (β . R)-1
D. F = α . β . (R)-1
E. F = R . (α . β)-1
Pembahasan
Diketahui :
Gaya tarik = F
Momen inersia katrol = β
Percepatan sudut katrol = α
Jari-jari katrol = R
Ditanya : Nilai F setara dengan….
Jawab :
Rumus hukum II Newton pada gerak rotasi :
Στ = β α ———- Persamaan 1
Keterangan rumus :
Στ = Resultan momen gaya (torsi)
β = Momen inersia
α = Percepatan sudut
Resultan momen gaya yang bekerja pada katrol :
Στ = F R ———-> Persamaan 2
Keterangan rumus :
F = gaya tarik
R = Jarak titik kerja gaya F ke sumbu rotasi = jari-jari katrol
Gantikan Στ pada persamaan 1 dengan Στ pada persamaan 2 :
Στ = β . α
F . R = β . α
F = (β . α) / R
F = β . α . (R-1)
Jawaban yang benar adalah D.
Momentum Sudut
10. Soal UN 1999/2000 No. 28
Sebuah partikel bermassa 0,2 gram bergerak melingkar dengan kecepatan sudut tetap 10 rad s-1. Jika jari-jari lintasan partikel 3 cm, maka momentum sudut partikel itu adalah …
A. 3 × 10–7 kg m2 s-1
B. 9 × 10–7 kg m2 s-1
C. 1,6 × 10–6 kg m2 s-1
D. 1,8 × 10–4 kg m2 s-1
E. 4,5 × 10–3 kg m2 s-1
Pembahasan
Diketahui :
Massa partikel (m) = 0,2 gram = 2 x 10-4 kg
Kecepatan sudut (ω) = 10 rad s-1
Jari-jari lintasan partikel (r) = 3 cm = 3 x 10-2 meter
Ditanya : Momentum sudut partikel
Jawab :
Rumus momentum sudut :
L = I ω
Keterangan : I momentum sudut, I = momen inersia, ω = kecepatan sudut
Momen inersia partikel :
I = m r2 = (2 x 10-4 )(3 x 10-2)2 = (2 x 10-4 )(9 x 10-4) = 18 x 10-8
Momentum sudut adalah :
L = I ω = (18 x 10-8)(10 rad s-1) = 18 x 10-7 kg m2 s-1
Tidak ada jawaban yang benar.
11. Soal UN 2005/2006
Seorang penari berputar, tangan terentang sepanjang 160 cm. Kemudian tangan dilipat menjadi 80 cm sepanjang siku. Jika kecepatan sudut putar dari penari itu tetap maka momentum liniernya …
A. tetap
B. menjadi 1/2 kali semula
C. menjadi 3/4 kali semula
D. menjadi 2 kali semula
E. menjadi 4 kali semula
Pembahasan
Diketahui :
Jari-jari 1 (r1) = 160 cm
Jari-jari 2 (r2) = 80 cm
Kecepatan sudut 1 (ω1) = ω
Kecepatan sudut 1 (ω2) = ω
Ditanya : Momentum linear
Jawab :
Kecepatan linear 1 :
v1 = r1 ω1 = (160 cm) ω
Kecepatan linear 2 :
v2 = r2 ω2 = (80 cm) ω
Momentum linear 1 :
p = m v1 = m (160 cm) ω
Momentum linear 2 :
p = m v2 = m (80 cm) ω
Jadi momentum linearnya menjadi 1/2 kali semula.
Jawaban yang benar adalah B.
Dinamika rotasi 222.50 KB
0 Response to "√Pembahasan Soal Dinamika Partikel ⊗ Full Pembahasanya"
Posting Komentar