√Contoh Soal Menentukan Kecepatan Akhir Gerak Parabola ⊗ Full Pembahasanya
Contoh soal menentukan kecepatan akhir gerak parabola
1. Bola disepak ke atas membentuk sudut 30o terhadap permukaan lapangan dengan kecepatan awal 14 m/s. Berapa kecepatan akhir bola ketika mencapai permukaan lapangan? Percepatan gravitasi = 10 m/s2
Pembahasan
Diketahui :
Sudut (θ) = 30o
Kecepatan awal (vo) = 14 m/s
Percepatan gravitasi (g) = 10 m/s2
Ditanya : Kecepatan akhir bola ketika mencapai permukaan lapangan
Jawab :
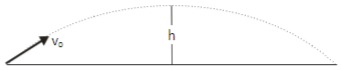 Lintasan bola seperti pada gambar.
Lintasan bola seperti pada gambar.
Komponen horisontal kecepatan awal bola :
vox = vo cos θ = (14 m/s)(cos 30o) = (14 m/s)(0,5√3) = 7√3 m/s
Komponen vertikal kecepatan awal bola :
voy = vo sin θ = (14 m/s)(sin 30o) = (14 m/s)(0,5) = 7 m/s
Gerak pada arah horisontal dianalisis seperti gerak lurus beraturan, sedangkan gerak pada arah vertikal dianalisis seperti gerak vertikal ke atas.
Kecepatan akhir bola pada arah vertikal
Setelah bergerak ke atas, bola bergerak kembali ke bawah. Kecepatan akhir bola ketika menyentuh tanah dihitung menggunakan rumus gerak vertikal ke atas.
Dalam menyelesaikan soal gerak vertikal ke atas, besaran vektor yang arahnya ke atas diberi tanda positif, besaran vektor yang arahnya ke bawah diberi tanda negatif.
Diketahui :
Kecepatan awal (vo) = 7 m/s (positif karena arah kecepatan ke atas)
Percepatan gravitasi (g) = -10 m/s2 (negatif karena arah percepatan gravitasi ke bawah)
Ketinggian (h) = 0 (bola kembali ke posisi semula sehingga perubahan ketinggian bernilai nol)
Ditanya : Kecepatan akhir bola (vt)
Jawab :
Diketahui vo, g, h dan ditanya vt sehingga rumus gerak vertikal ke atas yang digunakan adalah vt2 = vo2 + 2 g h
vt2 = vo2 + 2 g h = 72 + 2(-10)(0) = 49 – 0 = 49
vt = √49 = 7 m/s
Dapat disimpulkan bahwa kecepatan awal bola ketika bergerak ke atas sama dengan kecepatan akhir bola ketika mencapai permukaan lapangan.
Kecepatan akhir bola pada arah horisontal
Kecepatan awal pada arah horisontal adalah 7√3 m/s. Pada gerak lurus beraturan, kecepatan konstan sehingga kecepatan awal sama dengan kecepatan akhir. Jadi kecepatan akhir bola pada arah horisontal adalah 7√3 m/s.
Kecepatan akhir bola ketika mencapai permukaan lapangan
Kecepatan akhir bola merupakan gabungan dari kecepatan akhir pada arah horisontal dan kecepatan akhir pada arah vertikal.
![]()
Jika lintasan gerak parabola seperti pada gambar di atas maka kecepatan awal sama dengan kecepatan akhir.
2. Peluru ditembakkan ke atas dengan sudut kemiringan 30o terhadap horisontal dari suatu tempat yang berada 5 meter di atas permukaan tanah. Kecepatan awal peluru adalah 10 m/s. Berapa kecepatan akhir peluru ketika mencapai tanah ? Percepatan gravitasi 10 m/s2
Pembahasan
Diketahui :
Sudut (θ) = 30o
Ketinggian awal (ho) = 5 meter
Kecepatan awal (vo) = 10 m/s
Percepatan gravitasi (g) = 10 m/s2
Ditanya : Kecepatan akhir peluru ketika mencapai tanah
Jawab :
Komponen horisontal kecepatan awal bola :
vox = vo cos θ = (10 m/s)(cos 30o) = (10 m/s)(0,5√3) = 5√3 m/s
Komponen vertikal kecepatan awal bola :
voy = vo sin θ = (10 m/s)(sin 30o) = (10 m/s)(0,5) = 5 m/s
Gerak pada arah horisontal dianalisis seperti gerak lurus beraturan, sedangkan gerak pada arah vertikal dianalisis seperti gerak vertikal ke atas.
Kecepatan akhir peluru pada arah vertikal
Diketahui :
Kecepatan awal (vo) = 5 m/s (positif karena arah kecepatan ke atas)
Percepatan gravitasi (g) = -10 m/s2 (negatif karena arah percepatan gravitasi ke bawah)
Ketinggian (h) = -5 m (negatif karena permukaan tanah berada di bawah ketinggian awal)
Ditanya : Kecepatan akhir bola (vt)
Jawab :
Diketahui vo, g, h dan ditanya vt sehingga rumus gerak vertikal ke atas yang digunakan adalah vt2 = vo2 + 2 g h
vt2 = vo2 + 2 g h = 52 + 2(-10)(-5) = 25 + 100 = 125
vt = √125 m/s
Kecepatan akhir peluru pada arah horisontal
Kecepatan awal pada arah horisontal adalah 5√3 m/s. Pada gerak lurus beraturan, kecepatan konstan sehingga kecepatan awal sama dengan kecepatan akhir. Jadi kecepatan akhir peluru pada arah horisontal adalah 5√3 m/s.
Kecepatan akhir peluru ketika mencapai permukaan tanah
Kecepatan akhir peluru merupakan gabungan dari kecepatan akhir pada arah horisontal dan kecepatan akhir pada arah vertikal.
![]()
3. Kelereng dilemparkan horisontal ke kanan dari ketinggian 12 meter dengan kecepatan awal 8 m/s. Berapa kecepatan akhir kelereng ketika mengenai tanah ? Percepatan gravitasi = 10 m/s2
Pembahasan
Diketahui :
Ketinggian (h) = 12 meter
Kecepatan awal (vo) = 8 m/s
Percepatan gravitasi (g) = 10 m/s2
Ditanya : Kecepatan akhir (vt) kelereng ketika mengenai tanah
Jawab :
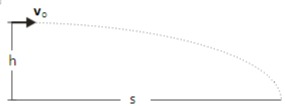 Lintasan gerak kelereng seperti pada gambar.
Lintasan gerak kelereng seperti pada gambar.
Kecepatan awal bola pada arah horisontal :
vox = vo = 8 m/s
Kecepatan awal bola pada arah vertikal :
voy = 0 m/s
Gerak pada arah horisontal dianalisis seperti gerak lurus beraturan, sedangkan gerak pada arah vertikal dianalisis seperti gerak jatuh bebas.
Kecepatan akhir kelereng pada arah vertikal
Kecepatan akhir dihitung menggunakan rumus gerak jatuh bebas.
Diketahui :
Percepatan gravitasi (g) = 10 m/s2
Ketinggian (h) = 12 m
Ditanya : Kecepatan akhir (vt)
Jawab :
Diketahui g, h dan ditanya vt sehingga rumus gerak jatuh bebas yang digunakan adalah vt2 = 2 g h
vt2 = 2 g h = 2(10)(12) = 240
vt = √240 m/s
Kecepatan akhir kelereng pada arah horisontal
Kecepatan awal pada arah horisontal adalah 8 m/s. Pada gerak lurus beraturan, kecepatan konstan sehingga kecepatan awal sama dengan kecepatan akhir. Jadi kecepatan akhir kelereng pada arah horisontal adalah 8 m/s.
Kecepatan akhir kelereng ketika mencapai permukaan tanah
Kecepatan akhir kelereng merupakan gabungan dari kecepatan akhir pada arah horisontal dan kecepatan akhir pada arah vertikal.
![]()
(Ukuran kertas : F4, Jumlah halaman : 15)
Materi Pembahasan Soal :
- Contoh soal menentukan komponen kecepatan awal gerak parabola
- Contoh soal menentukan ketinggian maksimum gerak parabola
- Contoh soal menentukan selang waktu gerak parabola
- Contoh soal menentukan posisi benda yang bergerak parabola
- Contoh soal menentukan jarak terjauh gerak parabola
- Contoh soal menentukan kecepatan akhir gerak parabola
Contoh soal menentukan ketinggian maksimum gerak parabola
1. Bola disepak ke atas membentuk sudut 60o terhadap permukaan lapangan. Jika kecepatan awal (vo) 10 m/s, berapa ketinggian maksimum bola ? Percepatan gravitasi = 10 m/s2
Pembahasan
Diketahui :
Sudut (θ) = 60o
Kecepatan awal (vo) = 10 m/s
Ditanya : Ketinggian maksimum (h)
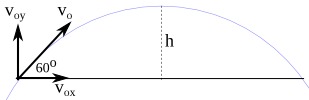 Jawab :
Jawab :
Lintasan gerak bola diilustrasikan oleh gambar.
Terlebih dahulu hitung kecepatan awal pada arah vertikal :
sin 60o = voy / vo
voy = vo sin 60o = (10)(sin 60o) = (10)(0,5√3) = 5√3 m/s
Setelah memperoleh nilai kecepatan awal pada arah vertikal (voy), sekarang hitung ketinggian maksimum menggunakan cara seperti menghitung ketinggian maksimum pada gerak vertikal ke atas. Dalam menyelesaikan soal gerak vertikal ke atas, besaran vektor yang arahnya ke atas diberi tanda positif, besaran vektor yang arahnya ke bawah diberi tanda negatif.
Diketahui :
Percepatan gravitasi (g) = -10 m/s2 (negatif karena arah percepatan gravitasi ke bawah)
Kecepatan awal pada arah vertikal (voy) = +5√3 m/s (positif karena arah kecepatan ke atas)
Kecepatan pada ketinggian maksimum (vty) = 0
Pada ketinggian maksimum, benda diam sesaat sebelum bergerak kembali ke bawah. Jadi pada ketinggian maksimum, kelajuan benda benilai nol.
Ditanya : Ketinggian maksimum (h)
Jawab :
Karena besaran yang diketahui adalah voy, g dan vty, sedangkan yang ditanyakan adalah h maka rumus gerak vertikal ke atas yang digunakan adalah :
vt2 = vo2 + 2 g h
Keterangan : vt = kelajuan akhir, vo = kelajuan awal, g = percepatan gravitasi, h = ketinggian maksimum.
Ketinggian maksimum :
vt2 = vo2 + 2 g h
02 = (5√3)2 + 2 (-10) h
0 = 25(3) – 20 h
0 = 75 – 20 h
75 = 20 h
h = 75 / 20
h = 3,75 meter
Jadi ketinggian maksimum yang dicapai bola adalah 3,75 meter.
2. Suatu benda dilempar ke atas dengan sudut kemiringan 30o terhadap horisontal, dari bangunan bertingkat yang berjarak 20 meter dari permukaan tanah. Kecepatan awal benda adalah 4 m/s. Tentukan ketinggian maksimum benda dihitung dari permukaan tanah! Percepatan gravitasi 10 m/s2.
Pembahasan
Diketahui :
Sudut (θ) = 30o
Ketinggian bangunan (h) = 20 meter
Kecepatan awal (vo) = 4 m/s
Percepatan gravitasi (g) = 10 m/s2
Ditanya : Ketinggian maksimum benda dihitung dari permukaan tanah (h)
Jawab :
Kecepatan awal benda pada arah vertikal :
sin 30o = voy / vo
voy = vo sin 30o = (4)(sin 30o) = (4)(0,5) = 2 m/s
Sekarang hitung ketinggian maksimum yang dicapai benda dari bangunan bertingkat menggunakan rumus gerak vertikal ke atas. Setelah itu dijumlahkan dengan ketinggian bangunan untuk memperoleh ketinggian total. Dalam menyelesaikan soal gerak vertikal ke atas, besaran vektor yang arahnya ke atas diberi tanda positif, besaran vektor yang arahnya ke bawah diberi tanda negatif.
Diketahui :
Percepatan gravitasi (g) = -10 m/s2 (negatif karena arah percepatan gravitasi ke bawah)
Kecepatan awal pada arah vertikal (voy) = +2 m/s (positif karena arah kecepatan ke atas)
Kecepatan benda pada ketinggian maksimum (vty) = 0
Ditanya : Ketinggian maksimum (h)
Jawab :
Ketinggian maksimum :
vt2 = vo2 + 2 g h
02 = 22 + 2 (-10) h
0 = 4 – 20 h
4 = 20 h
h = 4 / 20
h = 0,2 meter
Ketinggian maksimum yang dicapai bola dihitung dari permukaan tanah adalah 0,2 meter + 20 meter = 20,2 meter.
(Ukuran kertas : F4, Jumlah halaman : 15)
Materi Pembahasan Soal :
- Contoh soal menentukan komponen kecepatan awal gerak parabola
- Contoh soal menentukan ketinggian maksimum gerak parabola
- Contoh soal menentukan selang waktu gerak parabola
- Contoh soal menentukan posisi benda yang bergerak parabola
- Contoh soal menentukan jarak terjauh gerak parabola
- Contoh soal menentukan kecepatan akhir gerak parabola
Contoh soal menentukan ketinggian maksimum gerak parabola
1. Bola disepak ke atas membentuk sudut 60o terhadap permukaan lapangan. Jika kecepatan awal (vo) 10 m/s, berapa ketinggian maksimum bola ? Percepatan gravitasi = 10 m/s2
Pembahasan
Diketahui :
Sudut (θ) = 60o
Kecepatan awal (vo) = 10 m/s
Ditanya : Ketinggian maksimum (h)
 Jawab :
Jawab :
Lintasan gerak bola diilustrasikan oleh gambar.
Terlebih dahulu hitung kecepatan awal pada arah vertikal :
sin 60o = voy / vo
voy = vo sin 60o = (10)(sin 60o) = (10)(0,5√3) = 5√3 m/s
Setelah memperoleh nilai kecepatan awal pada arah vertikal (voy), sekarang hitung ketinggian maksimum menggunakan cara seperti menghitung ketinggian maksimum pada gerak vertikal ke atas. Dalam menyelesaikan soal gerak vertikal ke atas, besaran vektor yang arahnya ke atas diberi tanda positif, besaran vektor yang arahnya ke bawah diberi tanda negatif.
Diketahui :
Percepatan gravitasi (g) = -10 m/s2 (negatif karena arah percepatan gravitasi ke bawah)
Kecepatan awal pada arah vertikal (voy) = +5√3 m/s (positif karena arah kecepatan ke atas)
Kecepatan pada ketinggian maksimum (vty) = 0
Pada ketinggian maksimum, benda diam sesaat sebelum bergerak kembali ke bawah. Jadi pada ketinggian maksimum, kelajuan benda benilai nol.
Ditanya : Ketinggian maksimum (h)
Jawab :
Karena besaran yang diketahui adalah voy, g dan vty, sedangkan yang ditanyakan adalah h maka rumus gerak vertikal ke atas yang digunakan adalah :
vt2 = vo2 + 2 g h
Keterangan : vt = kelajuan akhir, vo = kelajuan awal, g = percepatan gravitasi, h = ketinggian maksimum.
Ketinggian maksimum :
vt2 = vo2 + 2 g h
02 = (5√3)2 + 2 (-10) h
0 = 25(3) – 20 h
0 = 75 – 20 h
75 = 20 h
h = 75 / 20
h = 3,75 meter
Jadi ketinggian maksimum yang dicapai bola adalah 3,75 meter.
2. Suatu benda dilempar ke atas dengan sudut kemiringan 30o terhadap horisontal, dari bangunan bertingkat yang berjarak 20 meter dari permukaan tanah. Kecepatan awal benda adalah 4 m/s. Tentukan ketinggian maksimum benda dihitung dari permukaan tanah! Percepatan gravitasi 10 m/s2.
Pembahasan
Diketahui :
Sudut (θ) = 30o
Ketinggian bangunan (h) = 20 meter
Kecepatan awal (vo) = 4 m/s
Percepatan gravitasi (g) = 10 m/s2
Ditanya : Ketinggian maksimum benda dihitung dari permukaan tanah (h)
Jawab :
Kecepatan awal benda pada arah vertikal :
sin 30o = voy / vo
voy = vo sin 30o = (4)(sin 30o) = (4)(0,5) = 2 m/s
Sekarang hitung ketinggian maksimum yang dicapai benda dari bangunan bertingkat menggunakan rumus gerak vertikal ke atas. Setelah itu dijumlahkan dengan ketinggian bangunan untuk memperoleh ketinggian total. Dalam menyelesaikan soal gerak vertikal ke atas, besaran vektor yang arahnya ke atas diberi tanda positif, besaran vektor yang arahnya ke bawah diberi tanda negatif.
Diketahui :
Percepatan gravitasi (g) = -10 m/s2 (negatif karena arah percepatan gravitasi ke bawah)
Kecepatan awal pada arah vertikal (voy) = +2 m/s (positif karena arah kecepatan ke atas)
Kecepatan benda pada ketinggian maksimum (vty) = 0
Ditanya : Ketinggian maksimum (h)
Jawab :
Ketinggian maksimum :
vt2 = vo2 + 2 g h
02 = 22 + 2 (-10) h
0 = 4 – 20 h
4 = 20 h
h = 4 / 20
h = 0,2 meter
Ketinggian maksimum yang dicapai bola dihitung dari permukaan tanah adalah 0,2 meter + 20 meter = 20,2 meter.
(Ukuran kertas : F4, Jumlah halaman : 15)
Materi Pembahasan Soal :
- Contoh soal menentukan komponen kecepatan awal gerak parabola
- Contoh soal menentukan ketinggian maksimum gerak parabola
- Contoh soal menentukan selang waktu gerak parabola
- Contoh soal menentukan posisi benda yang bergerak parabola
- Contoh soal menentukan jarak terjauh gerak parabola
- Contoh soal menentukan kecepatan akhir gerak parabola

0 Response to "√Contoh Soal Menentukan Kecepatan Akhir Gerak Parabola ⊗ Full Pembahasanya"
Posting Komentar