√Contoh Soal Energi Kinetik Rotasi ⊗ Full Pembahasanya

Pembahasan Soal MIPA , Baik dari segi perhitungan serta rumus singkatnya, sangatlah dibutuhkan untuk membantu dalam menyelesaikan permasalahan yang dihadapi oleh setiap siswa.Kebanyakan dari siswa itu kurang menyukainya karena mereka menganggapnya sangatlah rumit dan susah dengan berbagai rumus yang ada.

√Contoh Soal Energi Kinetik Rotasi ⊗ Full Pembahasanya

Dan jika kita lihat dari sisi yang positif, MIPA -Matemarika dan csnya jika kita nalar dari segi logika sebenarnya sangatlagh mudah. Dan kita tidak perlu menghapal rumusnya. Sebab pada dasarnya MIPA meruapakan ilmu pasti yang memang sudah di tentukan dan di golongkan solusi dari permasalahan yang ada,.

Trik Menyukai MIPA : kita jangan anggap MIPA itu pelajaran yang membosankan,dan susah, saat belajar MIPA kita hubungankan dengan dengan kehidupan sehari-hari, belajar MIPA bisa kita buat ke sebuah cerita yang menarik

Contoh soal energi kinetik rotasi

1. Benda mempunyai momen inersia 1 kg m2 berotasi pada sumbu tetap dengan kecepatan sudut 2 rad/s. Berapa energi kinetik rotasi benda tersebut ?

Pembahasan
Diketahui :
Momen inersia (I) = 1 kg m2
Kecepatan sudut (ω) = 2 rad/s
Ditanya : Energi kinetik rotasi (EK)
Jawab :
Rumus energi kinetik rotasi :
EK = 1/2 I ω2
Keterangan : EK = energi kinetik rotasi (kg m2/s2), I = momen inersia (kg m2), ω = kecepatan sudut (rad/s)

Energi kinetik rotasi :
EK = 1/2 I ω2 = 1/2 (1)(2)2 = 1/2 (1)(4) = 2 Joule

2. Katrol cakram pejal bermassa 20 kg dan berjari-jari 0,2 meter. Jika katrol bergerak rotasi pada porosnya dengan kecepatan sudut konstan 4 rad/sekon, berapa energi kinetik rotasi katrol ?

Pembahasan
Diketahui :
Massa katrol cakram pejal (m) = 20 kilogram
Jari-jari katrol cakram pejal (r) = 0,2 meter
Kecepatan sudut (ω) = 4 radian/sekon
Ditanya : Berapa energi kinetik rotasi katrol
Jawab :
Rumus momen inersia cakram pejal jika berotasi pada poros seperti pada gambar :
I = 1/2 m r2
Keterangan : I = momen inersia (kg m2), m = massa (kg), r = jari-jari (meter)
Momen inersia cakram pejal :
I = 1/2 (20)(0,2)2 = (10)(0,04) = 0,4 kg m2

Energi kinetik rotasi katrol :
EK = 1/2 I ω2 = 1/2 (0,4)(4)2 = (0,2)(16) = 3,2 Joule

3. Bola pejal (padat) bermassa 10 kg dan berjari-jari 0,1 meter berotasi terhadap porosnya dengan kecepatan sudut 10 rad/s. Tentukan energi kinetik rotasi bola pejal!
Pembahasan
Diketahui :
Massa bola pejal (m) = 10 kilogram
Jari-jari bola pejal (r) = 0,1 meter
Kecepatan sudut (ω) = 10 radian/sekon
Ditanya : Energi kinetik rotasi bola pejal
Jawab :
Rumus momen inersia bola pejal jika berotasi pada poros seperti pada gambar :
I = (2/5) m r2
Keterangan : I = momen inersia (kg m2), m = massa (kg), r = jari-jari (meter)
Momen inersia bola pejal :
I = (2/5)(10)(0,1)2 = (4)(0,01) = 0,04 kg m2

Energi kinetik rotasi bola pejal :
EK = 1/2 I ω2 = 1/2 (0,04)(10)2 = (0,02)(100) = 2 Joule

4. Sebuah partikel bermassa 0,5 kilogram bergerak melingkar dengan kecepatan sudut tetap 2 rad/s. Tentukan energi kinetik rotasi partikel jika jari-jari lintasan partikel 10 cm.
Pembahasan
Diketahui :
Massa partikel (m) = 0,5 kilogram
Jari-jari bola pejal (r) = 10 cm = 10/100 = 0,1 meter
Kecepatan sudut (ω) = 2 radian/sekon
Ditanya : Energi kinetik rotasi partikel
Jawab :
Rumus momen inersia partikel :
I = m r2 = (0,5)(0,1)2 = (0,5)(0,01) = 0,005 kg m2
Energi kinetik rotasi partikel :
EK = 1/2 I ω2 = 1/2 (0,005)(2)2 = 1/2 (0,005)(4) = (0,005)(2) = 0,01 Joule

5. Sebuah piringan berbentuk silinder pejal homogen mula-mula berputar pada porosnya dengan kelajuan sudut 4 rad/s. Massa dan jari-jari piringan 1 kg dan 0,5 m. Bila di atas piringan diletakkan cincin yang mempunyai massa 0,2 kg dan jari-jari 0,1 m, di mana pusat cincin tepat di atas pusat piring, maka piringan dan cincin akan bersama-sama berputar dengan energi kinetik rotasi sebesar…
Pembahasan
Diketahui :
Massa silinder pejal (m1) = 1 kilogram
Jari-jari silinder pejal (r1) = 0,5 meter
Kelajuan sudut silinder pejal (ω1) = 4 rad/s
Massa cincin (m2) = 0,2 kilogram
Jari-jari cincin (r2) = 0,1 meter
Ditanya : Energi kinetik rotasi silinder dan cincin
Jawab :
Terlebih dahulu hitung kecepatan sudut silinder dan cincin :
Momen inersia silinder pejal : I = 1⁄2 m1 r12 = 1⁄2 (1)(0,5)2 = (0,5)(0,25) = 0,125 kg m2
Momen inersia cincin : I = m r2 = (0,2)(0,1)2 = (0,2)(0,01) = 0,002 kg m2
Momen inersia silinder pejal dan cincin (I) = 0,125 + 0,002 = 0,127 kg m2

Momentum sudut awal (L1) = Momentum sudut akhir (L2)
I1 ω1 = I2 ω2
(0,125)(4) = (0,125 + 0,002)(ω2)
(0,5) = (0,127)(ω2)
ω2 = 0,5 : 0,127
ω2 = 4 rad/s

Hitung energi kinetik rotasi silinder dan cincin :
EK = 1/2 I ω2 = 1/2 (0,127)(4)2 = (0,127)(8) = 1,016 Joule

 

Contoh soal energi kinetik rotasi

1. Benda mempunyai momen inersia 1 kg m2 berotasi pada sumbu tetap dengan kecepatan sudut 2 rad/s. Berapa energi kinetik rotasi benda tersebut ?

Pembahasan
Diketahui :
Momen inersia (I) = 1 kg m2
Kecepatan sudut (ω) = 2 rad/s
Ditanya : Energi kinetik rotasi (EK)
Jawab :
Rumus energi kinetik rotasi :
EK = 1/2 I ω2
Keterangan : EK = energi kinetik rotasi (kg m2/s2), I = momen inersia (kg m2), ω = kecepatan sudut (rad/s)

Energi kinetik rotasi :
EK = 1/2 I ω2 = 1/2 (1)(2)2 = 1/2 (1)(4) = 2 Joule

2. Katrol cakram pejal bermassa 20 kg dan berjari-jari 0,2 meter. Jika katrol bergerak rotasi pada porosnya dengan kecepatan sudut konstan 4 rad/sekon, berapa energi kinetik rotasi katrol ?

Pembahasan
Diketahui :
Massa katrol cakram pejal (m) = 20 kilogram
Jari-jari katrol cakram pejal (r) = 0,2 meter
Kecepatan sudut (ω) = 4 radian/sekon
Ditanya : Berapa energi kinetik rotasi katrol
Jawab :
Rumus momen inersia cakram pejal jika berotasi pada poros seperti pada gambar :
I = 1/2 m r2
Keterangan : I = momen inersia (kg m2), m = massa (kg), r = jari-jari (meter)
Momen inersia cakram pejal :
I = 1/2 (20)(0,2)2 = (10)(0,04) = 0,4 kg m2

Energi kinetik rotasi katrol :
EK = 1/2 I ω2 = 1/2 (0,4)(4)2 = (0,2)(16) = 3,2 Joule

3. Bola pejal (padat) bermassa 10 kg dan berjari-jari 0,1 meter berotasi terhadap porosnya dengan kecepatan sudut 10 rad/s. Tentukan energi kinetik rotasi bola pejal!
Pembahasan
Diketahui :
Massa bola pejal (m) = 10 kilogram
Jari-jari bola pejal (r) = 0,1 meter
Kecepatan sudut (ω) = 10 radian/sekon
Ditanya : Energi kinetik rotasi bola pejal
Jawab :
Rumus momen inersia bola pejal jika berotasi pada poros seperti pada gambar :
I = (2/5) m r2
Keterangan : I = momen inersia (kg m2), m = massa (kg), r = jari-jari (meter)
Momen inersia bola pejal :
I = (2/5)(10)(0,1)2 = (4)(0,01) = 0,04 kg m2

Energi kinetik rotasi bola pejal :
EK = 1/2 I ω2 = 1/2 (0,04)(10)2 = (0,02)(100) = 2 Joule

4. Sebuah partikel bermassa 0,5 kilogram bergerak melingkar dengan kecepatan sudut tetap 2 rad/s. Tentukan energi kinetik rotasi partikel jika jari-jari lintasan partikel 10 cm.
Pembahasan
Diketahui :
Massa partikel (m) = 0,5 kilogram
Jari-jari bola pejal (r) = 10 cm = 10/100 = 0,1 meter
Kecepatan sudut (ω) = 2 radian/sekon
Ditanya : Energi kinetik rotasi partikel
Jawab :
Rumus momen inersia partikel :
I = m r2 = (0,5)(0,1)2 = (0,5)(0,01) = 0,005 kg m2
Energi kinetik rotasi partikel :
EK = 1/2 I ω2 = 1/2 (0,005)(2)2 = 1/2 (0,005)(4) = (0,005)(2) = 0,01 Joule

5. Sebuah piringan berbentuk silinder pejal homogen mula-mula berputar pada porosnya dengan kelajuan sudut 4 rad/s. Massa dan jari-jari piringan 1 kg dan 0,5 m. Bila di atas piringan diletakkan cincin yang mempunyai massa 0,2 kg dan jari-jari 0,1 m, di mana pusat cincin tepat di atas pusat piring, maka piringan dan cincin akan bersama-sama berputar dengan energi kinetik rotasi sebesar…
Pembahasan
Diketahui :
Massa silinder pejal (m1) = 1 kilogram
Jari-jari silinder pejal (r1) = 0,5 meter
Kelajuan sudut silinder pejal (ω1) = 4 rad/s
Massa cincin (m2) = 0,2 kilogram
Jari-jari cincin (r2) = 0,1 meter
Ditanya : Energi kinetik rotasi silinder dan cincin
Jawab :
Terlebih dahulu hitung kecepatan sudut silinder dan cincin :
Momen inersia silinder pejal : I = 1⁄2 m1 r12 = 1⁄2 (1)(0,5)2 = (0,5)(0,25) = 0,125 kg m2
Momen inersia cincin : I = m r2 = (0,2)(0,1)2 = (0,2)(0,01) = 0,002 kg m2
Momen inersia silinder pejal dan cincin (I) = 0,125 + 0,002 = 0,127 kg m2

Momentum sudut awal (L1) = Momentum sudut akhir (L2)
I1 ω1 = I2 ω2
(0,125)(4) = (0,125 + 0,002)(ω2)
(0,5) = (0,127)(ω2)
ω2 = 0,5 : 0,127
ω2 = 4 rad/s

Hitung energi kinetik rotasi silinder dan cincin :
EK = 1/2 I ω2 = 1/2 (0,127)(4)2 = (0,127)(8) = 1,016 Joule

 

Contoh soal energi potensial listrik

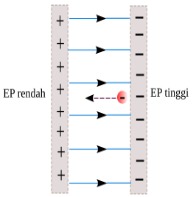
1. Elektron dipercepat dari keadaan diam melewati beda potensial 12 Volt. Berapa perubahan energi potensial elektron ?
Pembahasan
Diketahui :
Muatan 1 elektron (e) = -1,60 x 10-19 Coulomb
Beda potensial listrik = tegangan listrik (V) = 12 Volt
Ditanya : Perubahan energi potensial elektron (ΔEP)
Jawab :
ΔEP = q V = (-1,60 x 10-19 C)(12 V) = -19,2 x 10-19 Joule
Tanda negatif artinya energi potensial listrik berkurang. Ketika berada di dekat pelat bermuatan negatif, energi potensial listrik elektron bernilai maksimum. Setelah tiba di dekat pelat bermuatan positif, energi potensial listrik elektron bernilai minimum.

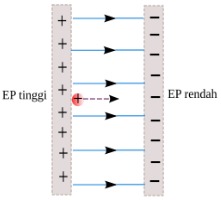
2. Dua pelat sejajar masing-masing bermuatan positif dan negatif. Medan listrik di antara kedua pelat adalah 500 Volt/meter. Jarak antara kedua pelat adalah 2 cm. Tentukan perubahan energi potensial proton ketika bergerak dari pelat bermuatan positif ke pelat bermuatan negatif!
Pembahasan
Diketahui :
Medan listrik di antara kedua pelat (E) = 500 Volt/meter
Jarak antara kedua pelat (s) = 2 cm = 0,02 meter
Muatan proton = +1,60 x 10-19 Coulomb
Ditanya : Perubahan energi potensial listrik (ΔEP)
Jawab :
Terlebih dahulu hitung beda potensial atau tegangan listrik :
V = E s
V = (500 Volt/meter)(0,02 meter)
V = 10 Volt

Perubahan energi potensial listrik :
ΔEP = q V
ΔEP = (1,60 x 10-19 C)(10 V)
ΔEP = 16 x 10-19 Joule
ΔEP = 1,6 x 10-18 Joule

Ketika berada di dekat pelat bermuatan positif, energi potensial listrik proton bernilai maksimum. Setelah tiba di dekat pelat bermuatan negatif, energi potensial listrik proton bernilai minimum. Jadi ketika bergerak dari pelat bermuatan positif ke pelat bermuatan negatif, energi potensial listrik proton berkurang.

3. Dua muatan disusun seperti pada gambar di bawah ini. Muatan di A adalah +9 μC dan muatan di B adalah -4 μC. Konstanta Coulomb (k) = 9 x 109 Nm2C−2, 1 μC = 10−6 C. Berapa perubahan energi potensial listrik muatan B jika bergerak ke muatan A ?
Pembahasan
Diketahui :
Muatan A (q1) = +9 μC = +9 x 10−6 C
Muatan B (q1) = -4 μC = -4 x 10−6 C
Konstanta Coulomb (k) = 9 x 109 Nm2C−2
Jarak antara muatan A dan B (r) = 10 cm = 0,1 meter = 10-1 meter
Ditanya : Perubahan energi potensial listrik muatan B jika bergerak ke muatan A
Jawab :

Muatan B bergerak ke muatan A sehingga energi potensial listriknya berkurang 2,4 Joule.
Hal ini menyerupai benda bermassa yang bergerak ke bawah mendekati bumi sehingga ketinggian dan energi potensial gravitasinya berkurang.

Ebook Pembahasan Soal Listrik Statis 220 kB

(Ukuran kertas : F4, Jumlah halaman : 16)

Materi Pembahasan Soal :

1. Contoh soal muatan listrik
2. Contoh soal hukum Coulomb
3. Contoh soal medan listrik
4. Contoh soal fluks listrik
5. Contoh soal energi potensial listrik
6. Contoh soal potensial listrik
7. Contoh soal kapasitor keping sejajar
8. Contoh soal kapasitor rangkaian paralel
9. Contoh soal kapasitor rangkaian seri
10. Contoh soal kapasitor rangkaian seri dan paralel

Tweet

Subscribe to receive free email updates: