√Hukum Gauss ⊗ Full Pembahasanya

Pembahasan Soal MIPA , Baik dari segi perhitungan serta rumus singkatnya, sangatlah dibutuhkan untuk membantu dalam menyelesaikan permasalahan yang dihadapi oleh setiap siswa.Kebanyakan dari siswa itu kurang menyukainya karena mereka menganggapnya sangatlah rumit dan susah dengan berbagai rumus yang ada.

√Hukum Gauss ⊗ Full Pembahasanya

Dan jika kita lihat dari sisi yang positif, MIPA -Matemarika dan csnya jika kita nalar dari segi logika sebenarnya sangatlagh mudah. Dan kita tidak perlu menghapal rumusnya. Sebab pada dasarnya MIPA meruapakan ilmu pasti yang memang sudah di tentukan dan di golongkan solusi dari permasalahan yang ada,.

Trik Menyukai MIPA : kita jangan anggap MIPA itu pelajaran yang membosankan,dan susah, saat belajar MIPA kita hubungankan dengan dengan kehidupan sehari-hari, belajar MIPA bisa kita buat ke sebuah cerita yang menarik

Hukum Gauss

Pada materi hukum Coulomb telah dipelajari gaya antar muatan listrik. Dalam ulasan mengenai medan listrik telah dibahas bentuk lain dari hukum Coulomb yang dinyatakan melalui persamaan F = q E, di mana F adalah gaya listrik, q adalah muatan listrik dan E adalah medan listrik. Dapat dikatakan bahwa hukum Coulomb merupakan hukum fisika yang menjelaskan hubungan antara muatan listrik (q) dengan medan listrik (E).

Hukum Gauss merupakan hukum fisika lainnya yang menjelaskan keterkaitan antara muatan listrik dengan medan listrik. Hukum Gauss dirumuskan oleh Carl Friedrich Gauss (1777-1855), fisikawan teoritis dan matematikawan berkebangsaan Jerman. Medan listrik yang ditimbulkan oleh satu atau beberapa muatan listrik dapat dihitung dengan mudah menggunakan hukum Coulomb, tetapi perhitungan menjadi lebih rumit jika yang ditentukan adalah medan listrik yang dihasilkan oleh suatu distribusi muatan listrik. Hukum Gauss menyediakan cara yang lebih mudah untuk menentukan medan listrik yang dihasilkan oleh suatu distribusi muatan listrik. Selain itu, jika diketahui medan listrik maka hukum Gauss dapat digunakan untuk menentukan distribusi muatan listrik yang menghasilkan medan listrik tersebut. Berikut ini diulas konsep dan rumus hukum Gauss.

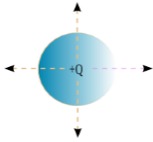Tinjau sebuah muatan listrik positif yang berada di pusat bola sebagaimana tampak pada gambar di samping. Apabila jari-jari bola adalah R maka kuat medan listrik yang dihasilkan muatan tersebut di seluruh permukaan bola adalah E = k Q / R2 dan luas permukaan bola adalah A = 4 π R2. Untuk memvisualisasikan medan listrik maka digambarkan garis-garis medan listrik tetapi pada gambar hanya diwakili empat garis medan listrik. Muatan listrik positif karenanya garis-garis medan listrik digambarkan keluar dari pusat bola di mana muatan listrik berada dan masing-masing garis medan listrik tegak lurus dengan permukaan bola yang dilewatinya. Semakin jauh dari muatan listrik, medan listrik semakin kecil sehingga jarak antara garis-garis medan listrik juga semakin jauh.

Fluks listrik yang menembus permukaan bola dihitung menggunakan rumus berikut :

Keterangan : Φ = fluks listrik, Q = muatan listrik, k = 9 x 109 N m2/C2, εo (permitivitas ruang hampa) = 8,85 x 10-12 C2/N m2, π = 3,14. Berdasarkan persamaan ini disimpulkan fluks listrik (Φ) yang melewati suatu permukaan berbentuk bola, sebanding dengan jumlah muatan listrik (Q) di dalamnya dan tidak bergantung pada jari-jari bola (R).

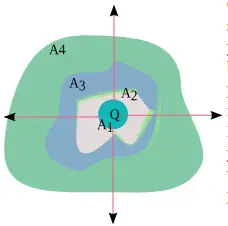Gambar di samping menunjukkan empat permukaan tertutup yang di dalamnya terdapat sebuah muatan listrik Q. Permukaan pertama berbentuk bola sedangkan permukaan lainnya mempunyai bentuk tak beraturan. Muatan listrik positif sehingga garis-garis medan listrik yang diwakili empat tanda panah digambarkan keluar dari muatan tersebut. Keempat garis medan listrik melewati permukaan berbentuk bola dan permukaan lainnya yang mempunyai bentuk tak beraturan. Pada ulasan mengenai fluks listrik dinyatakan bahwa fluks listrik merupakan garis-garis medan listrik yang menembus suatu luas permukaan tertentu. Garis medan listrik yang menembus keempat permukaan sama sehingga fluks listrik pada keempat permukaan mempunyai nilai yang sama. Fluks listrik yang menembus permukaan berbentuk bola setara dengan Φ = Q/εo , sehingga fluks listrik yang menembus permukaan lain yang bentuknya tak beraturan juga mempunyai nilai yang sama yakni Φ = Q/εo. Berdasarkan penjelasan ini dapat disimpulkan bahwa fluks listrik yang menembus suatu permukaan tertutup yang di dalamnya terdapat muatan listrik, tidak bergantung pada bentuk permukaan tersebut dan besarnya adalah Φ = 4 π k Q = Q/εo.

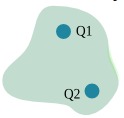Gambar di samping menunjukkan dua muatan listrik yang berada di dalam permukaan tertutup. Muatan Q1 dan Q2 positif sehingga jika digambarkan maka masing-masing muatan mempunyai garis medan listrik yang menembus keluar dari dalam permukaan tersebut. Fluks listrik total adalah jumlah total garis-garis medan listrik yang menembus keluar dari permukaan tertutup. Karena garis-garis medan listrik dari muatan Q1 setara dengan fluks listrik senilai Φ = Q1/εo dan garis-garis medan listrik dari muatan Q2 setara dengan fluks listrik senilai Φ = Q2/εo maka jumlah total garis-garis medan listrik sama dengan Q1/εo + Q2/εo = 1/εo (Q1 + Q2).

Berdasarkan penjelasan ini dapat disimpulkan bahwa fluks listrik total adalah 1/εo kali muatan listrik total dalam permukaan tertutup tersebut. Pernyataan ini merupakan hukum Gauss. Secara matematis :

Φtotal = 1/εo (Qtotal) ———- Persamaan hukum Gauss

Q total adalah jumlah total muatan listrik yang berada di dalam permukaan tertutup. Jika ada muatan listrik di luar permukaan tertutup maka muatan tersebut tidak diperhitungkan karena fluks listrik yang dihasilkannya bernilai nol. Fluks listriknya bernilai nol karena garis-garis medan listrik yang berasal dari muatan tersebut, menembus masuk ke dalam permukaan tertutup lalu keluar lagi sehingga resultan fluks bernilai nol. Permukaan tertutup pada hukum Gauss merupakan permukaan khayal yang dihadirkan untuk menghitung fluks listrik yang ditimbulkan oleh muatan listrik. Dengan kata lain, muatan-muatan listrik tidak harus berada di dalam suatu permukaan tertutup nyata. Hukum Gauss dapat digunakan untuk menentukan medan listrik jika distribusi muatan listrik diketahui atau dapat juga digunakan untuk menentukan distribusi muatan listrik apabila medan listrik diketahui. Penggunaan hukum Gauss untuk menyelesaikan berbagai soal dijelaskan dalam tulisan berjudul menentukan medan listrik menggunakan hukum Gauss.

Hukum Gauss

Pada materi hukum Coulomb telah dipelajari gaya antar muatan listrik. Dalam ulasan mengenai medan listrik telah dibahas bentuk lain dari hukum Coulomb yang dinyatakan melalui persamaan F = q E, di mana F adalah gaya listrik, q adalah muatan listrik dan E adalah medan listrik. Dapat dikatakan bahwa hukum Coulomb merupakan hukum fisika yang menjelaskan hubungan antara muatan listrik (q) dengan medan listrik (E).

Hukum Gauss merupakan hukum fisika lainnya yang menjelaskan keterkaitan antara muatan listrik dengan medan listrik. Hukum Gauss dirumuskan oleh Carl Friedrich Gauss (1777-1855), fisikawan teoritis dan matematikawan berkebangsaan Jerman. Medan listrik yang ditimbulkan oleh satu atau beberapa muatan listrik dapat dihitung dengan mudah menggunakan hukum Coulomb, tetapi perhitungan menjadi lebih rumit jika yang ditentukan adalah medan listrik yang dihasilkan oleh suatu distribusi muatan listrik. Hukum Gauss menyediakan cara yang lebih mudah untuk menentukan medan listrik yang dihasilkan oleh suatu distribusi muatan listrik. Selain itu, jika diketahui medan listrik maka hukum Gauss dapat digunakan untuk menentukan distribusi muatan listrik yang menghasilkan medan listrik tersebut. Berikut ini diulas konsep dan rumus hukum Gauss.

Tinjau sebuah muatan listrik positif yang berada di pusat bola sebagaimana tampak pada gambar di samping. Apabila jari-jari bola adalah R maka kuat medan listrik yang dihasilkan muatan tersebut di seluruh permukaan bola adalah E = k Q / R2 dan luas permukaan bola adalah A = 4 π R2. Untuk memvisualisasikan medan listrik maka digambarkan garis-garis medan listrik tetapi pada gambar hanya diwakili empat garis medan listrik. Muatan listrik positif karenanya garis-garis medan listrik digambarkan keluar dari pusat bola di mana muatan listrik berada dan masing-masing garis medan listrik tegak lurus dengan permukaan bola yang dilewatinya. Semakin jauh dari muatan listrik, medan listrik semakin kecil sehingga jarak antara garis-garis medan listrik juga semakin jauh.

Fluks listrik yang menembus permukaan bola dihitung menggunakan rumus berikut :

Keterangan : Φ = fluks listrik, Q = muatan listrik, k = 9 x 109 N m2/C2, εo (permitivitas ruang hampa) = 8,85 x 10-12 C2/N m2, π = 3,14. Berdasarkan persamaan ini disimpulkan fluks listrik (Φ) yang melewati suatu permukaan berbentuk bola, sebanding dengan jumlah muatan listrik (Q) di dalamnya dan tidak bergantung pada jari-jari bola (R).

Gambar di samping menunjukkan empat permukaan tertutup yang di dalamnya terdapat sebuah muatan listrik Q. Permukaan pertama berbentuk bola sedangkan permukaan lainnya mempunyai bentuk tak beraturan. Muatan listrik positif sehingga garis-garis medan listrik yang diwakili empat tanda panah digambarkan keluar dari muatan tersebut. Keempat garis medan listrik melewati permukaan berbentuk bola dan permukaan lainnya yang mempunyai bentuk tak beraturan. Pada ulasan mengenai fluks listrik dinyatakan bahwa fluks listrik merupakan garis-garis medan listrik yang menembus suatu luas permukaan tertentu. Garis medan listrik yang menembus keempat permukaan sama sehingga fluks listrik pada keempat permukaan mempunyai nilai yang sama. Fluks listrik yang menembus permukaan berbentuk bola setara dengan Φ = Q/εo , sehingga fluks listrik yang menembus permukaan lain yang bentuknya tak beraturan juga mempunyai nilai yang sama yakni Φ = Q/εo. Berdasarkan penjelasan ini dapat disimpulkan bahwa fluks listrik yang menembus suatu permukaan tertutup yang di dalamnya terdapat muatan listrik, tidak bergantung pada bentuk permukaan tersebut dan besarnya adalah Φ = 4 π k Q = Q/εo.

Gambar di samping menunjukkan dua muatan listrik yang berada di dalam permukaan tertutup. Muatan Q1 dan Q2 positif sehingga jika digambarkan maka masing-masing muatan mempunyai garis medan listrik yang menembus keluar dari dalam permukaan tersebut. Fluks listrik total adalah jumlah total garis-garis medan listrik yang menembus keluar dari permukaan tertutup. Karena garis-garis medan listrik dari muatan Q1 setara dengan fluks listrik senilai Φ = Q1/εo dan garis-garis medan listrik dari muatan Q2 setara dengan fluks listrik senilai Φ = Q2/εo maka jumlah total garis-garis medan listrik sama dengan Q1/εo + Q2/εo = 1/εo (Q1 + Q2).

Berdasarkan penjelasan ini dapat disimpulkan bahwa fluks listrik total adalah 1/εo kali muatan listrik total dalam permukaan tertutup tersebut. Pernyataan ini merupakan hukum Gauss. Secara matematis :

Φtotal = 1/εo (Qtotal) ———- Persamaan hukum Gauss

Q total adalah jumlah total muatan listrik yang berada di dalam permukaan tertutup. Jika ada muatan listrik di luar permukaan tertutup maka muatan tersebut tidak diperhitungkan karena fluks listrik yang dihasilkannya bernilai nol. Fluks listriknya bernilai nol karena garis-garis medan listrik yang berasal dari muatan tersebut, menembus masuk ke dalam permukaan tertutup lalu keluar lagi sehingga resultan fluks bernilai nol. Permukaan tertutup pada hukum Gauss merupakan permukaan khayal yang dihadirkan untuk menghitung fluks listrik yang ditimbulkan oleh muatan listrik. Dengan kata lain, muatan-muatan listrik tidak harus berada di dalam suatu permukaan tertutup nyata. Hukum Gauss dapat digunakan untuk menentukan medan listrik jika distribusi muatan listrik diketahui atau dapat juga digunakan untuk menentukan distribusi muatan listrik apabila medan listrik diketahui. Penggunaan hukum Gauss untuk menyelesaikan berbagai soal dijelaskan dalam tulisan berjudul menentukan medan listrik menggunakan hukum Gauss.

Hukum I Kirchhoff

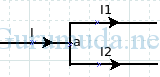Hukum I Kirchhoff disebut juga hukum titik cabang menyatakan bahwa arus listrik yang masuk ke suatu titik cabang sama dengan arus listrik yang keluar dari titik cabang tersebut. Titik cabang pada rangkaian listrik merupakan titik di mana dua atau lebih dari dua konduktor bertemu, seperti titik a pada gambar di samping.

I adalah arus listrik yang masuk ke titik cabang, sedangkan I1 dan I2 adalah arus listrik yang keluar dari titik cabang, I = I1 + I2. Contoh lain, amati gambar di bawah.

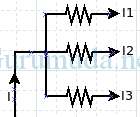I adalah arus listrik yang masuk, sedangkan I1, I2 dan I3 adalah arus listrik yang keluar, I = I1 + I2 + I3.

Hukum I Kirchhoff didasarkan pada hukum kekekalan muatan listrik yang menyatakan bahwa muatan bersifat kekal, sehingga muatan listrik yang masuk harus sama dengan muatan listrik yang keluar, tidak ada muatan listrik yang hilang. Arus listrik merupakan muatan listrik yang mengalir selama selang waktu tertentu. Karena muatan listrik kekal maka arus listrik yang masuk ke suatu titik cabang sama dengan arus listrik yang keluar dari titik cabang tersebut.

Hukum I Kirchhoff dikemukakan oleh Gustav Kirchhoff (1824-1887), seorang fisikawan Jerman.

Contoh soal 1 :

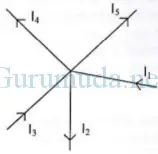I1 = 2 Ampere, I2 = 3 Ampere, I3 = 5 Ampere, I4 = 3 Ampere. Tentukan I5!

Pembahasan

I masuk = I keluar

I1 + I3 = I2 + I4 + I5

2 A + 5 A = 3 A + 3 A + I5

7 A = 6 A + I5

I5 = 7 A – 6 A

I5 = 1 Ampere

Contoh soal 2 :

I = 10 Ampere, I1 = 2 Ampere, I2 = 4 Ampere. Tentukan I3!

Pembahasan

I masuk = I keluar

I = I1 + I2 + I3

10 A = 2 A + 4 A + I3

10 A = 6 A + I3

I3 = 10 A – 6 A

I3 = 4 Ampere

Tweet

Subscribe to receive free email updates: