√Hukum Coulomb ⊗ Full Pembahasanya

Pembahasan Soal MIPA , Baik dari segi perhitungan serta rumus singkatnya, sangatlah dibutuhkan untuk membantu dalam menyelesaikan permasalahan yang dihadapi oleh setiap siswa.Kebanyakan dari siswa itu kurang menyukainya karena mereka menganggapnya sangatlah rumit dan susah dengan berbagai rumus yang ada.

√Hukum Coulomb ⊗ Full Pembahasanya

Dan jika kita lihat dari sisi yang positif, MIPA -Matemarika dan csnya jika kita nalar dari segi logika sebenarnya sangatlagh mudah. Dan kita tidak perlu menghapal rumusnya. Sebab pada dasarnya MIPA meruapakan ilmu pasti yang memang sudah di tentukan dan di golongkan solusi dari permasalahan yang ada,.

Trik Menyukai MIPA : kita jangan anggap MIPA itu pelajaran yang membosankan,dan susah, saat belajar MIPA kita hubungankan dengan dengan kehidupan sehari-hari, belajar MIPA bisa kita buat ke sebuah cerita yang menarik

Hukum Coulomb

Pada tulisan mengenai muatan listrik dan jenis-jenis muatan listrik diterangkan bahwa muatan listrik sejenis saling tolak menolak sedangkan muatan listrik tak sejenis saling tarik menarik. Dengan kata lain benda bermuatan positif tarik menarik dengan benda bermuatan negatif, benda bermuatan positif tolak menolak dengan benda bermuatan positif, dan benda bermuatan negatif tolak menolak dengan benda bermuatan negatif. Peristiwa ini menunjukkan adanya gaya listrik yang bekerja pada benda bermuatan positif dan benda bermuatan negatif. Faktor-faktor apa yang mempengaruhi besar gaya listrik antara benda bermuatan listrik ?

Fisikawan berkebangsaan Perancis bernama Charles Coulomb (1736-1806) melakukan serangkaian eksperimen pada tahun 1780-an untuk menyelidiki faktor-faktor yang mempengaruhi besar gaya listrik antara benda bermuatan listrik. Alat yang digunakan oleh Coulomb menyerupai alat yang digunakan Cavendish untuk menyelidiki konstanta gravitasi, dinamakan timbangan torsi. Coulomb menyelidiki gaya listrik karenanya Ia menggunakan dua bola logam bermuatan listrik sedangkan Cavendish menyelidiki gaya gravitasi karenanya Ia menggunakan dua bola bermassa yang tidak bermuatan listrik.

Cara kerja timbangan torsi  
 
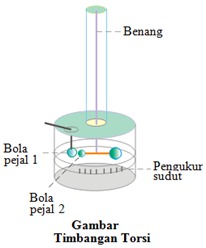Cara kerja timbangan torsi berkaitan dengan pokok bahasan torsi atau momen gaya pada bab dinamika rotasi.
Ruang dalam timbangan torsi hampa udara untuk menghindari muatan listrik pada bola pejal berpindah ke udara. Penentuan jumlah muatan listrik pada bola pejal dilakukan menggunakan cara berikut. Pada mulanya bola pejal A dijadikan bermuatan listrik melalui konduksi atau gesekan. Bola pejal A yang telah bermuatan listrik dihubungkan dengan bola pejal B yang masih netral menggunakan konduktor listrik hingga muatan listrik bola pejal A terbagi merata dengan bola pejal B. Jika jumlah muatan listrik bola pejal A adalah ½ maka jumlah muatan listrik bola pejal B adalah ½ . Selanjutnya bola pejal B dan bola pejal C dihubungkan dengan konduktor listrik hingga muatan listrik bola pejal B terbagi merata dengan bola pejal C. Jika jumlah muatan listrik bola pejal B adalah ¼ maka jumlah muatan listrik bola pejal C adalah ¼ . Jumlah muatan listrik dan jenis muatan listrik yang dimiliki bola pejal 1 dan bola pejal 2 diperoleh dengan cara seperti ini.

Bola pejal 1 dan bola pejal 2 bermuatan listrik sehingga kedua bola pejal saling tolak menolak jika kedua bola bermuatan listrik sejenis atau saling tarik menarik bila kedua bola bermuatan listrik tak sejenis. Adanya gaya tarik atau gaya tolak antara kedua bola pejal bermuatan listrik menyebabkan bola pejal 2 berotasi. Sudut tempuh bola pejal 2 diukur untuk mengetahui gaya listrik yang bekerja pada kedua bola pejal.

Faktor-faktor yang mempengaruhi gaya listrik

Berdasarkan eksperimen yang dilakukan menggunakan timbangan torsi, Coulomb menemukan beberapa hal.
– Pada percobaan ini, jarak antara kedua bola pejal selalu sama. Ketika jumlah muatan listrik pada bola pejal 1 adalah 1 dan jumlah muatan listrik pada bola pejal 2 adalah 1 maka gaya listrik yang bekerja pada kedua bola pejal adalah 1. Ketika jumlah muatan listrik pada bola pejal 1 adalah 2 dan jumlah muatan listrik pada bola pejal 2 adalah 2 maka gaya listrik yang bekerja pada kedua bola pejal adalah 4. Coulomb menyimpulkan bahwa besar gaya listrik yang bekerja pada kedua bola pejal sebanding dengan hasil kali jumlah muatan kedua bola pejal (F ≈ q1 q2).
– Pada percobaan ini, jumlah muatan kedua bola pejal selalu sama. Jika jarak antara kedua bola pejal adalah 1 maka gaya listrik yang bekerja pada kedua bola pejal adalah 1. Bila jarak jarak antara kedua bola pejal adalah 2 maka gaya listrik yang bekerja pada kedua bola pejal adalah ¼. Coulomb menyimpulkan bahwa besar gaya listrik yang bekerja pada kedua bola pejal berbanding terbalik dengan kuadrat jarak (F ≈ 1 / r2)

Hukum Coulomb

Hukum Coulomb adalah salah satu hukum fisika yang menjelaskan hubungan antara gaya listrik, muatan listrik dan jarak antara muatan listrik. Hukum ini dirumuskan berdasarkan eksperimen yang dilakukan Coulomb sebagaimana telah dijelaskan pada tulisan sebelumnya.

Hukum Coulomb menyatakan bahwa besar gaya yang dikerjakan oleh suatu partikel bermuatan listrik pada partikel bermuatan listrik lainnya berbanding lurus dengan hasil kali jumlah muatan kedua partikel dan berbanding terbalik dengan kuadrat jarak antara kedua partikel bermuatan listrik. Gaya ini bekerja sepanjang garis lurus yang menghubungkan kedua partikel. Gaya listrik bersifat tolak menolak jika muatan listrik kedua partikel sejenis dan gaya listrik bersifat tarik menarik jika muatan listrik kedua partikel tak sejenis.

Hukum Coulumb dapat dinyatakan dalam persamaan matematis :
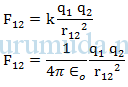Keterangan rumus :
F12 = gaya listrik antara partikel 1 dan partikel 2
q1 = jumlah muatan partikel 1
q2 = jumlah muatan listrik partikel 2
r12 = jarak antara partikel 1 dan partikel 2
(baca : epsilon nol) = 8,854 x 10-12 C2/N.m2
k = (konstanta Coulomb) = 9 x 109 N.m2/C2
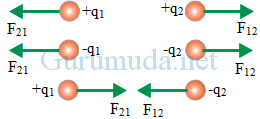F21 adalah gaya yang dikerjakan muatan q2 pada muatan q1, sedangkan F12 adalah gaya yang dikerjakan muatan q1 pada muatan q2. F21 dan F12 saling tolak menolak ketika muatan q1 dan q2 sejenis dan saling tarik menarik ketika muatan q1 dan q2 tak sejenis.
F21 dan F12 mempunyai nilai yang sama, berlawanan arah dan bekerja pada benda yang berbeda, karenanya kedua gaya ini merupakan pasangan gaya aksi reaksi.

Ebook Listrik Statis 438.87 KB

(Ukuran kertas : F4, Jumlah halaman : 36)

Materi Pembelajaran :

1. Muatan Listrik
2. Hukum Coulomb
3. Medan Listrik
4. Fluks Listrik
5. Hukum Gauss
6. Energi Potensial Listrik
7. Potensial Listrik
8. Kapasitor

Hukum gas ideal (Persamaan keadaan gas ideal)

Hukum-hukum gas antara lain hukum Boyle, hukum Charles dan hukum Gay‐Lussac tidak berlaku untuk semua kondisi gas maka analisis kita akan menjadi lebih sulit. Untuk mempermudah analisis, dibuat suatu model gas ideal. Gas ideal tidak ada dalam kehidupan sehari‐hari, gas ideal hanya bentuk sempurna yang sengaja dibuat untuk mempermudah analisis. Adanya konsep gas ideal ini juga sangat membantu kita dalam meninjau hubungan antara ketiga hukum gas tersebut.

Hubungan antara suhu, volume dan tekanan gas

Dengan berpedoman pada ketiga hukum gas di atas, kita bisa menurunkan hubungan yang lebih umum antara suhu, volume dan tekanan gas.

Jika persamaan 1, persamaan 2 dan persamaan 3 digabung menjadi satu, maka akan tampak seperti ini : PV ∝ T → Perbandingan 4

Perbandingan ini menyatakan bahwa tekanan (P) dan volume (V) sebanding dengan suhu mutlak (T).

Sebaliknya, volume (V) berbanding terbalik dengan tekanan (P).

Perbandingan 4 diubah menjadi persamaan :

Keterangan :

P1 = tekanan awal (Pa atau N/m2)

P2 = tekanan akhir (Pa atau N/m2)

V1 = volume awal (m3)

V2 = volume akhir (m3)

T1 = suhu awal (K)

T2 = suhu akhir (K)

(Pa = pascal, N = Newton, m2 = meter kuadrat, m3 = meter kubik, K = Kelvin)

Hubungan antara massa gas (m) dengan volume (V)

Ketika balon udara ditiup, semakin banyak udara yang dimasukkan, semakin kembung balon tersebut. Dengan kata lain, semakin besar massa gas, semakin besar volume balon. Kita bisa mengatakan bahwa massa gas (m) berbanding lurus dengan volume gas (V). Secara matematis :

V ∝ m → Perbandingan 5

Jika persamaan 4 digabung dengan persamaan 5 maka :

PV ∝ mT → Perbandingan 6

Jumlah mol (n)

1 mol = besarnya massa suatu zat yang setara dengan massa molekul zat tersebut. Massa dan massa molekul berbeda.

Contoh 1, massa molekul gas Oksigen (O2) = 16 u + 16 u = 32 u (setiap molekul oksigen berisi 2 atom Oksigen, di mana masing‐masing atom Oksigen mempunyai massa 16 u). Dengan demikian, 1 mol O2 mempunyai massa 32 gram. Atau massa molekul O2 = 32 gram/mol = 32 kg/kmol.

Contoh 2, massa molekul gas karbon monooksida (CO) = 12 u + 16 u = 28 u (setiap molekul karbon monooksida berisi 1 atom karbon (C) dan 1 atom oksigen (O). Massa 1 atom karbon = 12 u dan massa 1 atom Oksigen = 16 u. 12 u + 16 u = 28 u). Dengan demikian, 1 mol CO mempunyai massa 28 gram. Atau massa molekul CO = 28 gram/mol = 28 kg/kmol.

Contoh 3, massa molekul gas karbon dioksida (CO2) = [12 u + (2 x 16 u)] = [12 u + 32 u] = 44 u (setiap molekul karbon dioksida berisi 1 atom karbon (C ) dan 2 atom oksigen (O). Massa 1 atom Carbon = 12 u dan massa 1 atom oksigen = 16 u). Dengan demikian, 1 mol CO2 mempunyai massa 44 gram. Atau massa molekul CO2 = 44 gram/mol = 44 kg/kmol.

Jumlah mol (n) suatu zat = perbandingan massa zat tersebut dengan massa molekulnya. Secara matematis ditulis seperti ini :

Contoh 1 : hitung jumlah mol pada 64 gram O2

Massa O2 = 64 gram

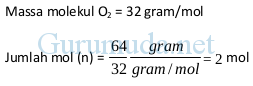
Contoh 2 : hitung jumlah mol pada 280 gram CO

Massa CO = 280 gram

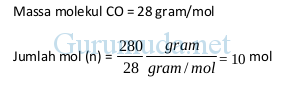
Contoh 3 : hitung jumlah mol pada 176 gram CO2

Massa CO2 = 176 gram

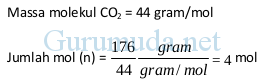
Konstanta gas universal (R)

Berdasarkan penelitian yang dilakukan para ilmuwan, ditemukan bahwa apabila jumlah mol (n) digunakan untuk menyatakan ukuran suatu zat maka konstanta perbandingan untuk setiap gas memiliki besar yang sama. Konstanta perbandingan yang dimaksud adalah konstanta gas universal (R).

R = 8,315 J/mol.K

= 8315 kJ/kmol.K

= 0,0821 (L.atm) / (mol.K)

= 1,99 kal / mol. K

(J = Joule, K = Kelvin, L = liter , atm = atmosfir, kal = kalori)

HUKUM GAS IDEAL (dalam jumlah mol)

Perbandingan di atas dapat diubah menjadi persamaan dengan memasukan jumlah mol (n) dan konstanta gas universal (R).

PV = nRT

Persamaan ini disebut hukum gas ideal atau persamaan keadaan gas ideal.

Keterangan :

P = tekanan gas (N/m2)

V = volume gas (m3)

n = jumlah mol (mol)

R = konstanta gas universal (R = 8,315 J/mol.K)

T = suhu mutlak gas (K )

Dalam penyelesaian soal, Anda akan menemukan istilah STP. STP merupakan singkatan dari Standard Temperature and Pressure atau Temperatur dan Tekanan Standar.

Temperatur standar (T) = 0 oC = 273 K

Tekanan standar (P) = 1 atm = 1,013 x 105 N/m2 = 1,013 x 102 kPa = 101 kPa

Dalam menyelesaikan soal‐soal hukum gas, suhu harus dinyatakan dalam skala Kelvin (K).

Apabila tekanan gas masih berupa tekanan ukur, ubah terlebih dahulu menjadi tekanan absolut.

Tekanan absolut = tekanan atmosfir + tekanan ukur (tekanan atmosfir = tekanan udara luar)

Jika yang diketahui adalah tekanan atmosfir (tidak ada tekanan ukur), langsung selesaikan soal tersebut.

Contoh soal 1 :

Pada tekanan atmosfir (101 kPa), suhu gas karbon dioksida = 20 oC dan volumenya = 2 liter. Apabila tekanan diubah menjadi 201 kPa dan suhu dinaikkan menjadi 40 oC, hitung volume akhir gas karbon dioksida tersebut

Pembahasan

Diketahui :

P1 = 101 kPa

P2 = 201 kPa

T1 = 20 oC + 273 K = 293 K

T2 = 40 oC + 273 K = 313 K

V1 = 2 liter

Ditanya : V2

Jawab :

Contoh soal 2 :

Tentukan volume 2 mol gas pada STP (anggap saja gas ini adalah gas ideal)

Pembahasan

Volume 2 mol gas pada STP (temperatur dan tekanan stadard) adalah 44,8 liter.

Contoh soal 3 :

Volume gas oksigen pada STP = 20 m3. Berapa massa gas oksigen ?

Pembahasan

Massa molekul oksigen = 32 gram/mol (massa 1 mol oksigen = 32 gram). Dengan demikian, massa gas oksigen adalah :

massa (m) = jumlah mol (n) x massa molekul

massa = (893 mol) x (32 gram/mol) = 28576 gram = 28,576 kg

Contoh soal 4 :

Sebuah tangki berisi 4 liter gas oksigen (O2). Suhu gas oksigen tersebut = 20 oC dan tekanan terukurnya = 20 x 105 N/m2. Tentukan massa gas oksigen tersebut (massa molekul oksigen = 32 kg/kmol = 32 gram/mol)

Pembahasan

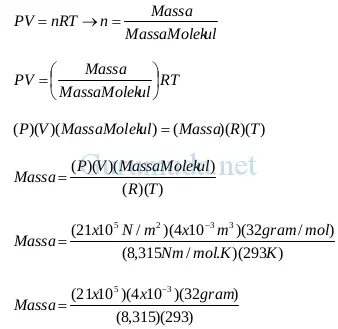
HUKUM GAS IDEAL (Dalam jumlah molekul)

Apabila kita menyatakan ukuran zat tidak dalam bentuk massa (m), tapi dalam jumlah mol (n), maka konstanta gas universal (R) berlaku untuk semua gas. Hal ini pertama kali ditemukan oleh Amedeo Avogadro (1776‐1856), ilmuwan Italia.

Avogadro mengatakan bahwa ketika volume, tekanan dan suhu setiap gas sama, maka setiap gas tersebut memiliki jumlah molekul yang sama.

Kalimat yang dicetak tebal miring disebut hipotesa Avogadro. Hipotesa atau dugaan Avogadro sesuai dengan kenyataan bahwa konstanta R sama untuk semua gas. Berikut ini beberapa pembuktiannya :

Pertama, jika kita menyelesaikan soal menggunakan persamaan hukum gas ideal (PV = nRT), kita akan menemukan bahwa ketika jumlah mol (n) sama, tekanan dan suhu juga sama, maka volume semua gas akan bernilai sama, apabila kita menggunakan konstanta gas universal (R = 8,315 J/mol.K). Pada STP, setiap gas yang memiliki jumlah mol (n) yang sama akan memiliki volume yang sama. Volume 1 mol gas pada STP = 22,4 liter. Volume 2 mol gas = 44,8 liter. Volume 3 mol gas = 67,2 liter. Dan seterusnya… ini berlaku untuk semua gas.

Kedua, jumlah molekul dalam 1 mol sama untuk semua gas. Jumlah molekul dalam 1 mol = jumlah molekul per mol = bilangan avogadro (NA). Jadi bilangan Avogadro bernilai sama untuk semua gas.

Besarnya bilangan Avogadro diperoleh melalui pengukuran :

NA = 6,02 x 1023 molekul/mol

Untuk memperoleh jumlah total molekul (N), kita bisa mengalikan jumlah molekul per mol (NA) dengan jumlah mol (n).

Ini adalah persamaan hukum gas ideal dalam bentuk jumlah molekul.

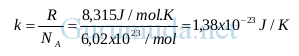
Keterangan :

P = Tekanan

V = Volume

N = Jumlah total molekul

k = Konstanta Boltzmann (k = 1,38 x 10‐23 J/K)

T = Suhu

Volume

1 liter (L) = 1000 mililiter (mL) = 1000 centimeter kubik (cm3)

1 liter (L) = 1 desimeter kubik (dm3) = 1 x 10‐3 m3

Tekanan

1 N/m2 = 1 Pa

1 atm = 1, 013 x 105 N/m2 = 1,013 x 105 Pa = 1,013 x 102 kPa = 101,3 kPa (biasanya dipakai 101 kPa)

Pa = pascal

atm = atmosfir

Hukum gas ideal (Persamaan keadaan gas ideal)

Hukum-hukum gas antara lain hukum Boyle, hukum Charles dan hukum Gay‐Lussac tidak berlaku untuk semua kondisi gas maka analisis kita akan menjadi lebih sulit. Untuk mempermudah analisis, dibuat suatu model gas ideal. Gas ideal tidak ada dalam kehidupan sehari‐hari, gas ideal hanya bentuk sempurna yang sengaja dibuat untuk mempermudah analisis. Adanya konsep gas ideal ini juga sangat membantu kita dalam meninjau hubungan antara ketiga hukum gas tersebut.

Hubungan antara suhu, volume dan tekanan gas

Dengan berpedoman pada ketiga hukum gas di atas, kita bisa menurunkan hubungan yang lebih umum antara suhu, volume dan tekanan gas.

Jika persamaan 1, persamaan 2 dan persamaan 3 digabung menjadi satu, maka akan tampak seperti ini : PV ∝ T → Perbandingan 4

Perbandingan ini menyatakan bahwa tekanan (P) dan volume (V) sebanding dengan suhu mutlak (T).

Sebaliknya, volume (V) berbanding terbalik dengan tekanan (P).

Perbandingan 4 diubah menjadi persamaan :

Keterangan :

P1 = tekanan awal (Pa atau N/m2)

P2 = tekanan akhir (Pa atau N/m2)

V1 = volume awal (m3)

V2 = volume akhir (m3)

T1 = suhu awal (K)

T2 = suhu akhir (K)

(Pa = pascal, N = Newton, m2 = meter kuadrat, m3 = meter kubik, K = Kelvin)

Hubungan antara massa gas (m) dengan volume (V)

Ketika balon udara ditiup, semakin banyak udara yang dimasukkan, semakin kembung balon tersebut. Dengan kata lain, semakin besar massa gas, semakin besar volume balon. Kita bisa mengatakan bahwa massa gas (m) berbanding lurus dengan volume gas (V). Secara matematis :

V ∝ m → Perbandingan 5

Jika persamaan 4 digabung dengan persamaan 5 maka :

PV ∝ mT → Perbandingan 6

Jumlah mol (n)

1 mol = besarnya massa suatu zat yang setara dengan massa molekul zat tersebut. Massa dan massa molekul berbeda.

Contoh 1, massa molekul gas Oksigen (O2) = 16 u + 16 u = 32 u (setiap molekul oksigen berisi 2 atom Oksigen, di mana masing‐masing atom Oksigen mempunyai massa 16 u). Dengan demikian, 1 mol O2 mempunyai massa 32 gram. Atau massa molekul O2 = 32 gram/mol = 32 kg/kmol.

Contoh 2, massa molekul gas karbon monooksida (CO) = 12 u + 16 u = 28 u (setiap molekul karbon monooksida berisi 1 atom karbon (C) dan 1 atom oksigen (O). Massa 1 atom karbon = 12 u dan massa 1 atom Oksigen = 16 u. 12 u + 16 u = 28 u). Dengan demikian, 1 mol CO mempunyai massa 28 gram. Atau massa molekul CO = 28 gram/mol = 28 kg/kmol.

Contoh 3, massa molekul gas karbon dioksida (CO2) = [12 u + (2 x 16 u)] = [12 u + 32 u] = 44 u (setiap molekul karbon dioksida berisi 1 atom karbon (C ) dan 2 atom oksigen (O). Massa 1 atom Carbon = 12 u dan massa 1 atom oksigen = 16 u). Dengan demikian, 1 mol CO2 mempunyai massa 44 gram. Atau massa molekul CO2 = 44 gram/mol = 44 kg/kmol.

Jumlah mol (n) suatu zat = perbandingan massa zat tersebut dengan massa molekulnya. Secara matematis ditulis seperti ini :

Contoh 1 : hitung jumlah mol pada 64 gram O2

Massa O2 = 64 gram

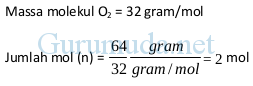
Contoh 2 : hitung jumlah mol pada 280 gram CO

Massa CO = 280 gram

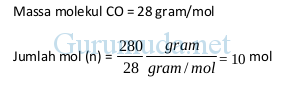
Contoh 3 : hitung jumlah mol pada 176 gram CO2

Massa CO2 = 176 gram

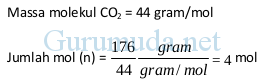
Konstanta gas universal (R)

Berdasarkan penelitian yang dilakukan para ilmuwan, ditemukan bahwa apabila jumlah mol (n) digunakan untuk menyatakan ukuran suatu zat maka konstanta perbandingan untuk setiap gas memiliki besar yang sama. Konstanta perbandingan yang dimaksud adalah konstanta gas universal (R).

R = 8,315 J/mol.K

= 8315 kJ/kmol.K

= 0,0821 (L.atm) / (mol.K)

= 1,99 kal / mol. K

(J = Joule, K = Kelvin, L = liter , atm = atmosfir, kal = kalori)

HUKUM GAS IDEAL (dalam jumlah mol)

Perbandingan di atas dapat diubah menjadi persamaan dengan memasukan jumlah mol (n) dan konstanta gas universal (R).

PV = nRT

Persamaan ini disebut hukum gas ideal atau persamaan keadaan gas ideal.

Keterangan :

P = tekanan gas (N/m2)

V = volume gas (m3)

n = jumlah mol (mol)

R = konstanta gas universal (R = 8,315 J/mol.K)

T = suhu mutlak gas (K )

Dalam penyelesaian soal, Anda akan menemukan istilah STP. STP merupakan singkatan dari Standard Temperature and Pressure atau Temperatur dan Tekanan Standar.

Temperatur standar (T) = 0 oC = 273 K

Tekanan standar (P) = 1 atm = 1,013 x 105 N/m2 = 1,013 x 102 kPa = 101 kPa

Dalam menyelesaikan soal‐soal hukum gas, suhu harus dinyatakan dalam skala Kelvin (K).

Apabila tekanan gas masih berupa tekanan ukur, ubah terlebih dahulu menjadi tekanan absolut.

Tekanan absolut = tekanan atmosfir + tekanan ukur (tekanan atmosfir = tekanan udara luar)

Jika yang diketahui adalah tekanan atmosfir (tidak ada tekanan ukur), langsung selesaikan soal tersebut.

Contoh soal 1 :

Pada tekanan atmosfir (101 kPa), suhu gas karbon dioksida = 20 oC dan volumenya = 2 liter. Apabila tekanan diubah menjadi 201 kPa dan suhu dinaikkan menjadi 40 oC, hitung volume akhir gas karbon dioksida tersebut

Pembahasan

Diketahui :

P1 = 101 kPa

P2 = 201 kPa

T1 = 20 oC + 273 K = 293 K

T2 = 40 oC + 273 K = 313 K

V1 = 2 liter

Ditanya : V2

Jawab :

Contoh soal 2 :

Tentukan volume 2 mol gas pada STP (anggap saja gas ini adalah gas ideal)

Pembahasan

Volume 2 mol gas pada STP (temperatur dan tekanan stadard) adalah 44,8 liter.

Contoh soal 3 :

Volume gas oksigen pada STP = 20 m3. Berapa massa gas oksigen ?

Pembahasan

Massa molekul oksigen = 32 gram/mol (massa 1 mol oksigen = 32 gram). Dengan demikian, massa gas oksigen adalah :

massa (m) = jumlah mol (n) x massa molekul

massa = (893 mol) x (32 gram/mol) = 28576 gram = 28,576 kg

Contoh soal 4 :

Sebuah tangki berisi 4 liter gas oksigen (O2). Suhu gas oksigen tersebut = 20 oC dan tekanan terukurnya = 20 x 105 N/m2. Tentukan massa gas oksigen tersebut (massa molekul oksigen = 32 kg/kmol = 32 gram/mol)

Pembahasan

HUKUM GAS IDEAL (Dalam jumlah molekul)

Apabila kita menyatakan ukuran zat tidak dalam bentuk massa (m), tapi dalam jumlah mol (n), maka konstanta gas universal (R) berlaku untuk semua gas. Hal ini pertama kali ditemukan oleh Amedeo Avogadro (1776‐1856), ilmuwan Italia.

Avogadro mengatakan bahwa ketika volume, tekanan dan suhu setiap gas sama, maka setiap gas tersebut memiliki jumlah molekul yang sama.

Kalimat yang dicetak tebal miring disebut hipotesa Avogadro. Hipotesa atau dugaan Avogadro sesuai dengan kenyataan bahwa konstanta R sama untuk semua gas. Berikut ini beberapa pembuktiannya :

Pertama, jika kita menyelesaikan soal menggunakan persamaan hukum gas ideal (PV = nRT), kita akan menemukan bahwa ketika jumlah mol (n) sama, tekanan dan suhu juga sama, maka volume semua gas akan bernilai sama, apabila kita menggunakan konstanta gas universal (R = 8,315 J/mol.K). Pada STP, setiap gas yang memiliki jumlah mol (n) yang sama akan memiliki volume yang sama. Volume 1 mol gas pada STP = 22,4 liter. Volume 2 mol gas = 44,8 liter. Volume 3 mol gas = 67,2 liter. Dan seterusnya… ini berlaku untuk semua gas.

Kedua, jumlah molekul dalam 1 mol sama untuk semua gas. Jumlah molekul dalam 1 mol = jumlah molekul per mol = bilangan avogadro (NA). Jadi bilangan Avogadro bernilai sama untuk semua gas.

Besarnya bilangan Avogadro diperoleh melalui pengukuran :

NA = 6,02 x 1023 molekul/mol

Untuk memperoleh jumlah total molekul (N), kita bisa mengalikan jumlah molekul per mol (NA) dengan jumlah mol (n).

Ini adalah persamaan hukum gas ideal dalam bentuk jumlah molekul.

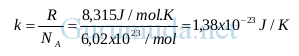
Keterangan :

P = Tekanan

V = Volume

N = Jumlah total molekul

k = Konstanta Boltzmann (k = 1,38 x 10‐23 J/K)

T = Suhu

Volume

1 liter (L) = 1000 mililiter (mL) = 1000 centimeter kubik (cm3)

1 liter (L) = 1 desimeter kubik (dm3) = 1 x 10‐3 m3

Tekanan

1 N/m2 = 1 Pa

1 atm = 1, 013 x 105 N/m2 = 1,013 x 105 Pa = 1,013 x 102 kPa = 101,3 kPa (biasanya dipakai 101 kPa)

Pa = pascal

atm = atmosfir

Tweet

Subscribe to receive free email updates: