√Fluks Listrik ⊗ Full Pembahasanya

Pembahasan Soal MIPA , Baik dari segi perhitungan serta rumus singkatnya, sangatlah dibutuhkan untuk membantu dalam menyelesaikan permasalahan yang dihadapi oleh setiap siswa.Kebanyakan dari siswa itu kurang menyukainya karena mereka menganggapnya sangatlah rumit dan susah dengan berbagai rumus yang ada.

√Fluks Listrik ⊗ Full Pembahasanya

Dan jika kita lihat dari sisi yang positif, MIPA -Matemarika dan csnya jika kita nalar dari segi logika sebenarnya sangatlagh mudah. Dan kita tidak perlu menghapal rumusnya. Sebab pada dasarnya MIPA meruapakan ilmu pasti yang memang sudah di tentukan dan di golongkan solusi dari permasalahan yang ada,.

Trik Menyukai MIPA : kita jangan anggap MIPA itu pelajaran yang membosankan,dan susah, saat belajar MIPA kita hubungankan dengan dengan kehidupan sehari-hari, belajar MIPA bisa kita buat ke sebuah cerita yang menarik

Fluks Listrik

Pada topik Medan listrik, telah dibahas pengertian dan rumus medan listrik yang dapat digunakan untuk menghitung kuat medan listrik yang dihasilkan oleh satu muatan listrik, beberapa muatan listrik atau oleh suatu distribusi muatan listrik. Perhitungan kuat medan listrik yang dihasilkan oleh sebuah muatan listrik atau dua buah muatan listrik mudah diselesaikan menggunakan rumus kuat medan listrik. Apabila yang dihitung adalah kuat medan listrik yang dihasilkan oleh suatu distribusi muatan listrik maka perhitungan lebih rumit jika digunakan rumus kuat medan listrik tetapi lebih mudah jika digunakan hukum Gauss. Sebelum mempelajari hukum Gauss secara mendalam, terlebih dahulu dipahami fluks listrik karena konsep fluks listrik digunakan dalam hukum Gauss.

Pengertian Fluks Listrik

Kata fluks berasal dari kata bahasa latin, fluere, yang artinya mengalir. Secara harafiah, fluks listrik dapat diartikan sebagai aliran medan listrik. Kata aliran di sini tidak menunjukkan medan listrik mengalir seperti air mengalir, tetapi menjelaskan adanya medan listrik yang mengarah ke arah tertentu. Pada topik Garis-garis medan listrik telah dijelaskan bahwa medan listrik divisualisasikan atau digambarkan menggunakan garis-garis medan listrik karenanya fluks listrik juga digambarkan berupa garis-garis medan listrik. Jadi fluks listrik merupakan garis-garis medan listrik yang melewati suatu luas permukaan tertentu, sebagaimana dicontohkan pada gambar di bawah.

Rumus Fluks Listrik

Secara matematis, fluks listrik adalah hasil kali antara medan listrik (E), luas permukaan (A) dan cosinus sudut antara 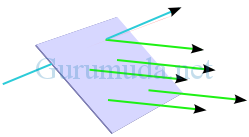garis medan listrik dengan garis normal yang tegak lurus permukaan.

Φ = E A cos θ ……………. (Persamaan 1)

Jika garis-garis medan listrik tegak lurus dengan luas permukaan yang dilewatinya seperti pada gambar, maka sudut
antara garis medan listrik dengan garis normal adalah 0o, di mana cos 0o = 1. Dengan demikian rumus fluks listrikberubah menjadi :

Φ = E A cos 0o = E A (1)
Φ = E A ……………. (Persamaan 2)

Berdasarkan rumus fluks listrik di atas disimpulkan beberapa hal. Pertama, fluks listrik bernilai maksimum ketika garis medan listrik tegak lurus dengan luas permukaan karena pada kondisi tersebut sudut antara garis medan listrik dengan garis normal adalah 0o, di mana nilai cosinus 0o adalah 1. Kedua, fluks listrik bernilai minimum ketika garis medan listrik sejajar dengan luas permukaan karena pada kondisi tersebut sudut antara garis medan listrik dengan garis normal adalah 90o, di mana nilai cosinus 90o adalah 0. Ketiga, fluks listrik bergantung pada medan listrik (E) dan luas permukaan (A). Selain luas permukaan berbentuk persegi seperti pada contoh di atas, luas permukaan juga bisa berbentuk bola dan lainnya.

Fluks Listrik pada Permukaan Tertutup

Fuks listrik yang dijelaskan sebelumnya menggunakan contoh permukaan terbuka (luas permukaan persegi atau persegi panjang). Bagaimana fluks listrik pada permukaan tertutup seperti kubus, balok atau bola ? Andaikan terdapat garis-garis medan listrik yang melewati balok seperti pada gambar di bawah.
Garis-garis medan listrik yang diberi warna biru berhimpit dengan permukaan atas dan bawah balok sehingga membentuk sudut 90o dengan garis normal permukaan atas dan bawah. Dengan demikian fluks listrik pada permukaan atas dan bawah balok adalah Φ = E A cos 90o = E A (0) = 0.

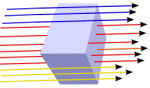Garis-garis medan listrik yang diberi warna kuning berhimpit dengan permukaan samping kanan dan kiri balok sehingga membentuk sudut 90o dengan garis normal permukaan samping kiri dan kanan. Dengan demikian fluks listrik pada permukaan samping kanan dan kiri balok adalah Φ = E A cos 90o = E A (0) = 0.
Garis-garis medan listrik yang diberi warna merah tegak lurus dengan permukaan depan dan belakang balok sehingga membentuk sudut 0o dengan garis normal permukaan depan dan belakang. Dengan demikian fluks listrik adalah Φ = E A cos 0o = E A (1) = E A.

Pada gambar di atas, tampak garis-garis medan listrik berwarna merah bergerak ke dalam balok lalu bergerak keluar dari balok. Ketika garis-garis medan listrik bergerak masuk ke balok seolah-olah terdapat muatan negatif di dalam balok maka fluks listrik bernilai negatif. Sebaliknya ketika garis-garis medan listrik bergerak ke luar dari balok seolah-olah terdapat muatan positif di dalam balok maka fluks listrik bernilai positif. Secara kualitatif atau tanpa perhitungan, jika jumlah garis medan listrik yang masuk ke balok sama dengan jumlah garis medan listrik yang keluar dari balok maka resultan fluks listrik bernilai nol. Secara kuantitatif atau menggunakan perhitungan, resultan fluks listrik yang melewati balok dihitung dengan cara berikut : fluks listrik masuk = Φ1 = – E A cos 0o = – E A (1) = -E A dan fluks listrik keluar = Φ2 = + E A cos 0o = + E A (1) = +E A. Fluks listrik total adalah Φ = -Φ1 + Φ2 = -E A + E A = 0.

Berdasarkan perhitungan di atas disimpulkan bahwa fluks listrik total yang melewati balok seperti pada gambar di atas bernilai nol. Bisa dikatakan bahwa fluks listrik total bernilai nol karena tidak ada muatan listrik dalam balok tersebut. Jadi apabila tidak ada muatan listrik dalam permukaan tertutup seperti balok, kubus, bola dan lainnya maka fluks listrik total bernilai nol. Bagaimana jika terdapat muatan listrik pada permukaan tertutup ?

Misalkan terdapat muatan listrik pada pusat bola sebagaimana tampak pada gambar di samping. Keempat garis medan listrik digambarkan mewakili garis-garis medan listrik lainnya yang bergerak keluar dari pusat bola tegak lurus permukaan bola. Masing-masing garis tegak lurus dengan permukaan bola yang dilewatinya sehingga membentuk sudut 0o dengan garis normal yang tegak lurus permukaan bola.

Fluks listrik pada bola :
Rumus kuat medan listrik adalah E = k Q / r2 dan rumus luas permukaan bola adalah A = 4 π r2 sehingga rumus fluks listrik berubah menjadi :

Jika muatan pada pusat bola adalah +2Q maka fluks listrik pada bola adalah

Berdasarkan rumus fluks listrik di atas disimpulkan bahwa jika terdapat muatan listrik di dalam permukaan tertutup berbentuk bola maka nilai fluks listrik pada bola tersebut tidak bergantung pada diameter atau jari-jari bola. Nilai fluks listrik adalah 4πk kali muatan listrik total di dalam bola tersebut atau 1/εo kali muatan listrik total di dalam bola tersebut.

Satuan Fluks Listrik

Rumus dasar fluks listrik adalah Φ = E A, di mana E adalah kuat medan listrik dan A adalah luas permukaan. Satuan medan listrik adalah Newton per Coulomb (N/C) dan satuan luas permukaan adalah meter kuadrat (m2) sehingga satuan fluks listrik adalah Newton meter kuadrat per Coulomb (Nm2/C).

Fluks Listrik

Pada topik Medan listrik, telah dibahas pengertian dan rumus medan listrik yang dapat digunakan untuk menghitung kuat medan listrik yang dihasilkan oleh satu muatan listrik, beberapa muatan listrik atau oleh suatu distribusi muatan listrik. Perhitungan kuat medan listrik yang dihasilkan oleh sebuah muatan listrik atau dua buah muatan listrik mudah diselesaikan menggunakan rumus kuat medan listrik. Apabila yang dihitung adalah kuat medan listrik yang dihasilkan oleh suatu distribusi muatan listrik maka perhitungan lebih rumit jika digunakan rumus kuat medan listrik tetapi lebih mudah jika digunakan hukum Gauss. Sebelum mempelajari hukum Gauss secara mendalam, terlebih dahulu dipahami fluks listrik karena konsep fluks listrik digunakan dalam hukum Gauss.

Pengertian Fluks Listrik

Kata fluks berasal dari kata bahasa latin, fluere, yang artinya mengalir. Secara harafiah, fluks listrik dapat diartikan sebagai aliran medan listrik. Kata aliran di sini tidak menunjukkan medan listrik mengalir seperti air mengalir, tetapi menjelaskan adanya medan listrik yang mengarah ke arah tertentu. Pada topik Garis-garis medan listrik telah dijelaskan bahwa medan listrik divisualisasikan atau digambarkan menggunakan garis-garis medan listrik karenanya fluks listrik juga digambarkan berupa garis-garis medan listrik. Jadi fluks listrik merupakan garis-garis medan listrik yang melewati suatu luas permukaan tertentu, sebagaimana dicontohkan pada gambar di bawah.

Rumus Fluks Listrik

Secara matematis, fluks listrik adalah hasil kali antara medan listrik (E), luas permukaan (A) dan cosinus sudut antara garis medan listrik dengan garis normal yang tegak lurus permukaan.

Φ = E A cos θ ……………. (Persamaan 1)

Jika garis-garis medan listrik tegak lurus dengan luas permukaan yang dilewatinya seperti pada gambar, maka sudut
antara garis medan listrik dengan garis normal adalah 0o, di mana cos 0o = 1. Dengan demikian rumus fluks listrikberubah menjadi :

Φ = E A cos 0o = E A (1)
Φ = E A ……………. (Persamaan 2)

Berdasarkan rumus fluks listrik di atas disimpulkan beberapa hal. Pertama, fluks listrik bernilai maksimum ketika garis medan listrik tegak lurus dengan luas permukaan karena pada kondisi tersebut sudut antara garis medan listrik dengan garis normal adalah 0o, di mana nilai cosinus 0o adalah 1. Kedua, fluks listrik bernilai minimum ketika garis medan listrik sejajar dengan luas permukaan karena pada kondisi tersebut sudut antara garis medan listrik dengan garis normal adalah 90o, di mana nilai cosinus 90o adalah 0. Ketiga, fluks listrik bergantung pada medan listrik (E) dan luas permukaan (A). Selain luas permukaan berbentuk persegi seperti pada contoh di atas, luas permukaan juga bisa berbentuk bola dan lainnya.

Fluks Listrik pada Permukaan Tertutup

Fuks listrik yang dijelaskan sebelumnya menggunakan contoh permukaan terbuka (luas permukaan persegi atau persegi panjang). Bagaimana fluks listrik pada permukaan tertutup seperti kubus, balok atau bola ? Andaikan terdapat garis-garis medan listrik yang melewati balok seperti pada gambar di bawah.
Garis-garis medan listrik yang diberi warna biru berhimpit dengan permukaan atas dan bawah balok sehingga membentuk sudut 90o dengan garis normal permukaan atas dan bawah. Dengan demikian fluks listrik pada permukaan atas dan bawah balok adalah Φ = E A cos 90o = E A (0) = 0.

Garis-garis medan listrik yang diberi warna kuning berhimpit dengan permukaan samping kanan dan kiri balok sehingga membentuk sudut 90o dengan garis normal permukaan samping kiri dan kanan. Dengan demikian fluks listrik pada permukaan samping kanan dan kiri balok adalah Φ = E A cos 90o = E A (0) = 0.
Garis-garis medan listrik yang diberi warna merah tegak lurus dengan permukaan depan dan belakang balok sehingga membentuk sudut 0o dengan garis normal permukaan depan dan belakang. Dengan demikian fluks listrik adalah Φ = E A cos 0o = E A (1) = E A.

Pada gambar di atas, tampak garis-garis medan listrik berwarna merah bergerak ke dalam balok lalu bergerak keluar dari balok. Ketika garis-garis medan listrik bergerak masuk ke balok seolah-olah terdapat muatan negatif di dalam balok maka fluks listrik bernilai negatif. Sebaliknya ketika garis-garis medan listrik bergerak ke luar dari balok seolah-olah terdapat muatan positif di dalam balok maka fluks listrik bernilai positif. Secara kualitatif atau tanpa perhitungan, jika jumlah garis medan listrik yang masuk ke balok sama dengan jumlah garis medan listrik yang keluar dari balok maka resultan fluks listrik bernilai nol. Secara kuantitatif atau menggunakan perhitungan, resultan fluks listrik yang melewati balok dihitung dengan cara berikut : fluks listrik masuk = Φ1 = – E A cos 0o = – E A (1) = -E A dan fluks listrik keluar = Φ2 = + E A cos 0o = + E A (1) = +E A. Fluks listrik total adalah Φ = -Φ1 + Φ2 = -E A + E A = 0.

Berdasarkan perhitungan di atas disimpulkan bahwa fluks listrik total yang melewati balok seperti pada gambar di atas bernilai nol. Bisa dikatakan bahwa fluks listrik total bernilai nol karena tidak ada muatan listrik dalam balok tersebut. Jadi apabila tidak ada muatan listrik dalam permukaan tertutup seperti balok, kubus, bola dan lainnya maka fluks listrik total bernilai nol. Bagaimana jika terdapat muatan listrik pada permukaan tertutup ?

Misalkan terdapat muatan listrik pada pusat bola sebagaimana tampak pada gambar di samping. Keempat garis medan listrik digambarkan mewakili garis-garis medan listrik lainnya yang bergerak keluar dari pusat bola tegak lurus permukaan bola. Masing-masing garis tegak lurus dengan permukaan bola yang dilewatinya sehingga membentuk sudut 0o dengan garis normal yang tegak lurus permukaan bola.

Fluks listrik pada bola :
Rumus kuat medan listrik adalah E = k Q / r2 dan rumus luas permukaan bola adalah A = 4 π r2 sehingga rumus fluks listrik berubah menjadi :

Jika muatan pada pusat bola adalah +2Q maka fluks listrik pada bola adalah

Berdasarkan rumus fluks listrik di atas disimpulkan bahwa jika terdapat muatan listrik di dalam permukaan tertutup berbentuk bola maka nilai fluks listrik pada bola tersebut tidak bergantung pada diameter atau jari-jari bola. Nilai fluks listrik adalah 4πk kali muatan listrik total di dalam bola tersebut atau 1/εo kali muatan listrik total di dalam bola tersebut.

Satuan Fluks Listrik

Rumus dasar fluks listrik adalah Φ = E A, di mana E adalah kuat medan listrik dan A adalah luas permukaan. Satuan medan listrik adalah Newton per Coulomb (N/C) dan satuan luas permukaan adalah meter kuadrat (m2) sehingga satuan fluks listrik adalah Newton meter kuadrat per Coulomb (Nm2/C).

Garis-garis medan listrik

Medan listrik merupakan sesuatu yang ditimbulkan oleh muatan listrik dan mempengaruhi ruang di sekitar muatan listrik tersebut, di mana pengaruh medan listrik hanya dirasakan oleh muatan listrik lainnya. Ketika muatan listrik lain berada dalam medan listrik yang ditimbulkan oleh suatu muatan listrik maka muatan listrik lain merasakan pengaruh berupa gaya listrik.

Pengertian medan listrik di atas, sebagaimana telah dijelaskan pada tulisan tentang medan listrik, dapat dipahami dengan pikiran tetapi juga hanya dapat dibayangkan dalam pikiran. Untuk memvisualisasikan medan listrik maka dihadirkan garis-garis medan listrik. Garis-garis medan listrik adalah sekumpulan garis yang digambarkan di sekitar suatu muatan listrik untuk menunjukkan keberadaan medan listrik. Karena bertujuan menunjukan keberadaan medan listrik maka ada keterkaitan antara garis-garis tersebut dengan medan listrik. Dengan kata lain, besar dan arah medan listrik dapat dijelaskan melalui gambar garis-garis medan listrik.

Berikut ini keterkaitan antara arah dan kuat medan listrik dengan garis-garis medan listrik :

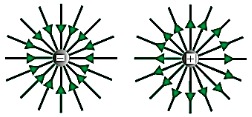Pertama, arah medan listrik menjauhi muatan positif dan mendekati muatan negatif. Dengan demikian, arah garis-garis medan listrik juga menjauhi muatan positif dan mendekati muatan negatif. Apabila muatan positif berdekatan dengan muatan negatif maka garis-garis medan listrik digambarkan keluar dari muatan positif menuju muatan negatif. Sebaliknya apabila muatan positif berdekatan dengan muatan positif, garis-garis medan listrik digambarkan keluar dari masing-masing muatan positif dan saling menjauhi.

Kedua, kuat medan listrik diwakili oleh jarak antara garis-garis medan listrik. Semakin dekat jarak antara garis-garis medan listrik, semakin besar kuat medan listrik dan semakin jauh jarak antara garis-garis medan listrik, semakin kecil kuat medan listrik.

Mengapa semakin dekat jarak antara garis, semakin besar kuat medan listrik ? Untuk memahami hal ini, cermati penjelasan berikut. Andaikan suatu muatan positif berada pada pusat bola dan garis-garis medan listrik menyebar keluar ke berbagai arah menembus permukaan bola. Apabila jumlah garis medan listrik adalah N dan luas permukaan bola adalah 4πr2 maka jumlah garis per satuan luas atau kerapatan garis adalah N/4πr2. Berdasarkan rumus ini, untuk N yang sama, bila r semakin kecil maka jarak antara garis semakin dekat dan jika r semakin besar maka jarak antara garis semakin jauh. Rumus kuat medan listrik E = kq/r2 juga menunjukan bahwa kuat medan listrik berbanding terbalik dengan kuadrat jarak. Jika r semakin kecil maka kuat medan listrik semakin besar dan bila r semakin besar maka kuat medan listrik semakin kecil.
Berdasarkan ulasan di atas dapat disimpulkan bahwa jika r semakin kecil (semakin dekat dengan muatan) maka kuat medan listrik semakin besar dan jarak antara garis juga semakin dekat. Sebaliknya bila r semakin besar (semakin jauh dari muatan) maka kuat medan listrik semakin kecil dan jarak antara garis juga semakin jauh.

Ketiga, jumlah garis medan listrik sebanding dengan kuat medan listrik. Semakin banyak garis medan listrik, semakin besar kuat medan listrik. Semakin sedikit garis medan listrik, semakin kecil kuat medan listrik.

Ebook Listrik Statis 438.87 KB

(Ukuran kertas : F4, Jumlah halaman : 36)

Materi Pembelajaran :

1. Muatan Listrik
2. Hukum Coulomb
3. Medan Listrik
4. Fluks Listrik
5. Hukum Gauss
6. Energi Potensial Listrik
7. Potensial Listrik
8. Kapasitor

Tweet

Subscribe to receive free email updates: