√Garis-garis Medan Listrik ⊗ Full Pembahasanya

Pembahasan Soal MIPA , Baik dari segi perhitungan serta rumus singkatnya, sangatlah dibutuhkan untuk membantu dalam menyelesaikan permasalahan yang dihadapi oleh setiap siswa.Kebanyakan dari siswa itu kurang menyukainya karena mereka menganggapnya sangatlah rumit dan susah dengan berbagai rumus yang ada.

√Garis-garis Medan Listrik ⊗ Full Pembahasanya

Dan jika kita lihat dari sisi yang positif, MIPA -Matemarika dan csnya jika kita nalar dari segi logika sebenarnya sangatlagh mudah. Dan kita tidak perlu menghapal rumusnya. Sebab pada dasarnya MIPA meruapakan ilmu pasti yang memang sudah di tentukan dan di golongkan solusi dari permasalahan yang ada,.

Trik Menyukai MIPA : kita jangan anggap MIPA itu pelajaran yang membosankan,dan susah, saat belajar MIPA kita hubungankan dengan dengan kehidupan sehari-hari, belajar MIPA bisa kita buat ke sebuah cerita yang menarik

Garis-garis medan listrik

Medan listrik merupakan sesuatu yang ditimbulkan oleh muatan listrik dan mempengaruhi ruang di sekitar muatan listrik tersebut, di mana pengaruh medan listrik hanya dirasakan oleh muatan listrik lainnya. Ketika muatan listrik lain berada dalam medan listrik yang ditimbulkan oleh suatu muatan listrik maka muatan listrik lain merasakan pengaruh berupa gaya listrik.

Pengertian medan listrik di atas, sebagaimana telah dijelaskan pada tulisan tentang medan listrik, dapat dipahami dengan pikiran tetapi juga hanya dapat dibayangkan dalam pikiran. Untuk memvisualisasikan medan listrik maka dihadirkan garis-garis medan listrik. Garis-garis medan listrik adalah sekumpulan garis yang digambarkan di sekitar suatu muatan listrik untuk menunjukkan keberadaan medan listrik. Karena bertujuan menunjukan keberadaan medan listrik maka ada keterkaitan antara garis-garis tersebut dengan medan listrik. Dengan kata lain, besar dan arah medan listrik dapat dijelaskan melalui gambar garis-garis medan listrik.

Berikut ini keterkaitan antara arah dan kuat medan listrik dengan garis-garis medan listrik :

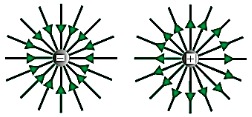Pertama, arah medan listrik menjauhi muatan positif dan mendekati muatan negatif. Dengan demikian, arah garis-garis medan listrik juga menjauhi muatan positif dan mendekati muatan negatif. Apabila muatan positif berdekatan dengan muatan negatif maka garis-garis medan listrik digambarkan keluar dari muatan positif menuju muatan negatif. Sebaliknya apabila muatan positif berdekatan dengan muatan positif, garis-garis medan listrik digambarkan keluar dari masing-masing muatan positif dan saling menjauhi.

Kedua, kuat medan listrik diwakili oleh jarak antara garis-garis medan listrik. Semakin dekat jarak antara garis-garis medan listrik, semakin besar kuat medan listrik dan semakin jauh jarak antara garis-garis medan listrik, semakin kecil kuat medan listrik.

Mengapa semakin dekat jarak antara garis, semakin besar kuat medan listrik ? Untuk memahami hal ini, cermati penjelasan berikut. Andaikan suatu muatan positif berada pada pusat bola dan garis-garis medan listrik menyebar keluar ke berbagai arah menembus permukaan bola. Apabila jumlah garis medan listrik adalah N dan luas permukaan bola adalah 4πr2 maka jumlah garis per satuan luas atau kerapatan garis adalah N/4πr2. Berdasarkan rumus ini, untuk N yang sama, bila r semakin kecil maka jarak antara garis semakin dekat dan jika r semakin besar maka jarak antara garis semakin jauh. Rumus kuat medan listrik E = kq/r2 juga menunjukan bahwa kuat medan listrik berbanding terbalik dengan kuadrat jarak. Jika r semakin kecil maka kuat medan listrik semakin besar dan bila r semakin besar maka kuat medan listrik semakin kecil.
Berdasarkan ulasan di atas dapat disimpulkan bahwa jika r semakin kecil (semakin dekat dengan muatan) maka kuat medan listrik semakin besar dan jarak antara garis juga semakin dekat. Sebaliknya bila r semakin besar (semakin jauh dari muatan) maka kuat medan listrik semakin kecil dan jarak antara garis juga semakin jauh.

Ketiga, jumlah garis medan listrik sebanding dengan kuat medan listrik. Semakin banyak garis medan listrik, semakin besar kuat medan listrik. Semakin sedikit garis medan listrik, semakin kecil kuat medan listrik.

Ebook Listrik Statis 438.87 KB

(Ukuran kertas : F4, Jumlah halaman : 36)

Materi Pembelajaran :

1. Muatan Listrik
2. Hukum Coulomb
3. Medan Listrik
4. Fluks Listrik
5. Hukum Gauss
6. Energi Potensial Listrik
7. Potensial Listrik
8. Kapasitor

Gaya gerak listrik (ggl) seri dan paralel

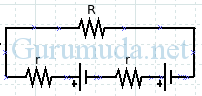Jika terdapat dua atau lebih dari dua sumber tegangan listrik (ggl) yang terangkai seperti pada gambar di samping, ggl tersebut terangkai seri.

Sumber tegangan listrik (ε) pengganti adalah :

ε = ε1 + ε2 + εn

Hambatan dalam (r) pengganti adalah :

r = r1 + r2 + rn

Kuat arus listrik yang mengalir melewati hambatan luar (R) adalah :

I = ε / (r + R)

Contoh soal :

Misalkan dua baterai masing-masing gglnya bernilai 1,5 Volt dan nilai hambatan dalam masing-masing baterai 0,1 Ω. Hambatan luar (R) = 10 Ω. Arah arus listrik searah putaran jarum jam.

Gunakan rumus sebelumnya :

ε = 1,5 + 1,5 = 3 Volt

r = 0,1 + 0,1 = 0,2 Ω

I = ε / (r + R) = 3 / (0,2 + 10)

I = 3 / 10,2

I = 0,294 Ampere

Gunakan hukum II Kirchhoff :

1,5 – 0,1 I + 1,5 – 0,1 I – 10 I = 0

3 – 0,2 I – 10 I = 0

3 – 10,2 I = 0

3 = 10,2 I

I = 3 / 10,2

I = 0,294 Ampere 

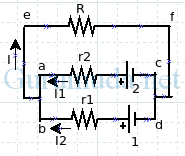Jika terdapat dua atau lebih dari dua sumber tegangan listrik (ggl) yang terangkai seperti pada gambar di samping, ggl tersebut terangkai paralel.

Sumber tegangan listrik (ε) pengganti adalah :

ε = ε1 = ε2 = εn

Hambatan dalam (r) pengganti adalah :

1/r = 1/r1 + 1/r2 + 1/rn

Kuat arus listrik yang mengalir melewati hambatan luar (R) adalah :

I = ε / (r + R)

Contoh soal :

Misalkan dua baterai masing-masing gglnya bernilai 1,5 Volt dan nilai hambatan dalam masing-masing baterai 0,1 Ω. Hambatan luar (R) = 10 Ω.

Gunakan rumus sebelumnya :

ε = 1,5 Volt

1/r = 1/0,1 + 1/0,1 = 2 / 0,1

r = 0,1 / 2 = 0,05 Ω

I = ε / (r + R) = 1,5 / (0,05 + 10) = 1,5 / 10,05

I = 0,149 Ampere

Gunakan hukum Kirchhoff

Terapkan hukum I Kirchhoff :

I1 + I2 = I ………. Persamaan 1

Analisis loop aefca. Arah loop searah putaran jarum jam. Terapkan hukum II Kirchhoff :

ε2 – I1 r2 – I R = 0

1,5 – 0,1 I1 – 10 I = 0

– 0,1 I1 = 10 I – 1,5

I1 = (10 I – 1,5 ) / – 0,1

I1 = -100 I + 15 ………. Persamaan 2

Analisis loop befdb. Arah loop searah putaran jarum jam. Terapkan hukum II Kirchhoff :

ε1 – I2 r1 – I R = 0

1,5 – 0,1 I2 – 10 I = 0

– 0,1 I2 = 10 I – 1,5

I2 = (10 I – 1,5) / – 0,1

I2 = -100 I + 15 ………. Persamaan 3

Subtitusikan persamaan 2 dan 3 ke persamaan 1 :

I1 + I2 = I

-100 I + 15 – 100 I + 15 = I

– 200 I + 30 = I

30 = I + 200 I

30 = 201 I

I = 30 / 201

I = 0,149 Ampere

Eliminasikan persamaan 2 daan 3 :

I1 = -100 I + 15

I2 = -100 I + 15

——————– –

I1 – I2 = 0

I1 = I2 ………. Persamaan 4

Karena I1 + I2 = I, di mana I1 = I2 maka I1 = I2 = 1/2 I = 1/2 (0,149) = 0,0745 Ampere.

Gaya gerak listrik (ggl) seri dan paralel

Jika terdapat dua atau lebih dari dua sumber tegangan listrik (ggl) yang terangkai seperti pada gambar di samping, ggl tersebut terangkai seri.

Sumber tegangan listrik (ε) pengganti adalah :

ε = ε1 + ε2 + εn

Hambatan dalam (r) pengganti adalah :

r = r1 + r2 + rn

Kuat arus listrik yang mengalir melewati hambatan luar (R) adalah :

I = ε / (r + R)

Contoh soal :

Misalkan dua baterai masing-masing gglnya bernilai 1,5 Volt dan nilai hambatan dalam masing-masing baterai 0,1 Ω. Hambatan luar (R) = 10 Ω. Arah arus listrik searah putaran jarum jam.

Gunakan rumus sebelumnya :

ε = 1,5 + 1,5 = 3 Volt

r = 0,1 + 0,1 = 0,2 Ω

I = ε / (r + R) = 3 / (0,2 + 10)

I = 3 / 10,2

I = 0,294 Ampere

Gunakan hukum II Kirchhoff :

1,5 – 0,1 I + 1,5 – 0,1 I – 10 I = 0

3 – 0,2 I – 10 I = 0

3 – 10,2 I = 0

3 = 10,2 I

I = 3 / 10,2

I = 0,294 Ampere 

Jika terdapat dua atau lebih dari dua sumber tegangan listrik (ggl) yang terangkai seperti pada gambar di samping, ggl tersebut terangkai paralel.

Sumber tegangan listrik (ε) pengganti adalah :

ε = ε1 = ε2 = εn

Hambatan dalam (r) pengganti adalah :

1/r = 1/r1 + 1/r2 + 1/rn

Kuat arus listrik yang mengalir melewati hambatan luar (R) adalah :

I = ε / (r + R)

Contoh soal :

Misalkan dua baterai masing-masing gglnya bernilai 1,5 Volt dan nilai hambatan dalam masing-masing baterai 0,1 Ω. Hambatan luar (R) = 10 Ω.

Gunakan rumus sebelumnya :

ε = 1,5 Volt

1/r = 1/0,1 + 1/0,1 = 2 / 0,1

r = 0,1 / 2 = 0,05 Ω

I = ε / (r + R) = 1,5 / (0,05 + 10) = 1,5 / 10,05

I = 0,149 Ampere

Gunakan hukum Kirchhoff

Terapkan hukum I Kirchhoff :

I1 + I2 = I ………. Persamaan 1

Analisis loop aefca. Arah loop searah putaran jarum jam. Terapkan hukum II Kirchhoff :

ε2 – I1 r2 – I R = 0

1,5 – 0,1 I1 – 10 I = 0

– 0,1 I1 = 10 I – 1,5

I1 = (10 I – 1,5 ) / – 0,1

I1 = -100 I + 15 ………. Persamaan 2

Analisis loop befdb. Arah loop searah putaran jarum jam. Terapkan hukum II Kirchhoff :

ε1 – I2 r1 – I R = 0

1,5 – 0,1 I2 – 10 I = 0

– 0,1 I2 = 10 I – 1,5

I2 = (10 I – 1,5) / – 0,1

I2 = -100 I + 15 ………. Persamaan 3

Subtitusikan persamaan 2 dan 3 ke persamaan 1 :

I1 + I2 = I

-100 I + 15 – 100 I + 15 = I

– 200 I + 30 = I

30 = I + 200 I

30 = 201 I

I = 30 / 201

I = 0,149 Ampere

Eliminasikan persamaan 2 daan 3 :

I1 = -100 I + 15

I2 = -100 I + 15

——————– –

I1 – I2 = 0

I1 = I2 ………. Persamaan 4

Karena I1 + I2 = I, di mana I1 = I2 maka I1 = I2 = 1/2 I = 1/2 (0,149) = 0,0745 Ampere.

Tweet

Subscribe to receive free email updates: